Bayes news: teaching the Beta-Binomial using real and fake headlines

UKCOTS 2025 University of Glasgow

Dr. Laurie Baker, Bates College; Dr. Jim Scott, Colby College; Dr. Mine Dogucu, UC Irvine

Outline

• Introduce the Course Context
• Introduce the Activity
• Next Steps

Course Context

• Target Course: Intro to Probability and Statistics or Bayesian Statistics Course

• Student Background:

• Basic probability concepts (e.g., probability of success/failure)

• What a probability distribution represents

• Familiarity with the concept of conditional probability

• Some prior experience with R programming

Activity Overview

• Goal: Show how priors, data, and posteriors interact with a real example

CNN (the Cable News Network) is widely considered a reputable news source. The Onion, on the other hand, is (according to Wikipedia) “an American news satire organization.

How well do people distinguish real news stories published on cnn.com from fake news stories published on theonion.com?

Learning Objectives

• Define and distinguish between prior and posterior distributions.
• Use the Beta distribution to construct prior beliefs about a probability.
• Apply Bayesian updating to revise beliefs with observed data.
• Interpret summary statistics (mean, mode, standard deviation) of Beta distributions.
• Reflect on how prior information and data interact to shape posterior conclusions.

Activity Sequence

1. Introduce the Context
2. Construct and Visualize Priors
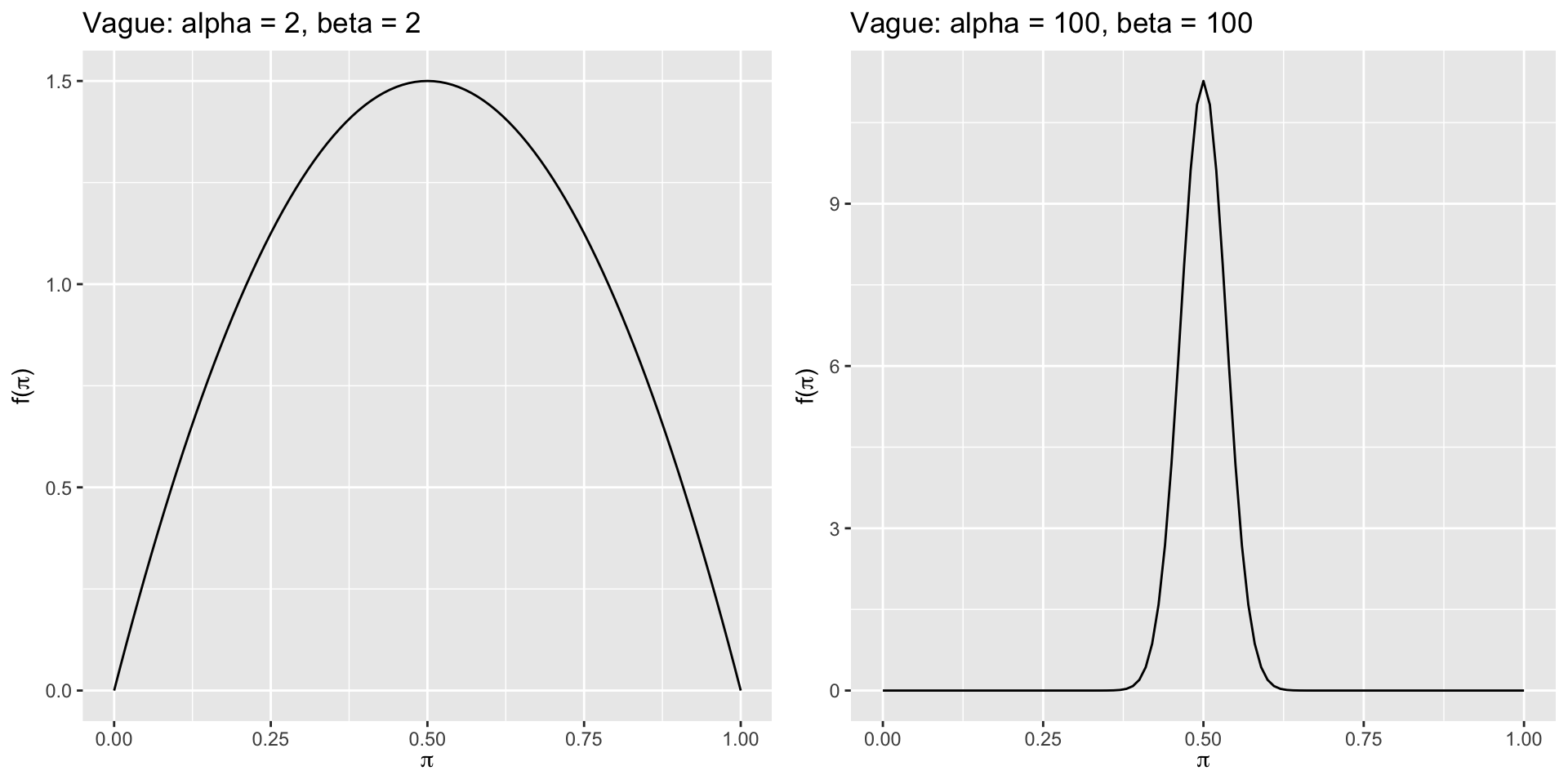
3. Discuss Vague vs. Informative Priors
4. Take the Quiz
5. Update Priors with Data and Visualize Posterior
6. Update Priors with Class Data and Visualize Posterior
7. Compare Posteriors from Different Priors
8. Discussion questions

1. Introduce priors

Let \(\pi\) be the proportion of correct answers a person guesses right in the CNN vs the Onion quiz.

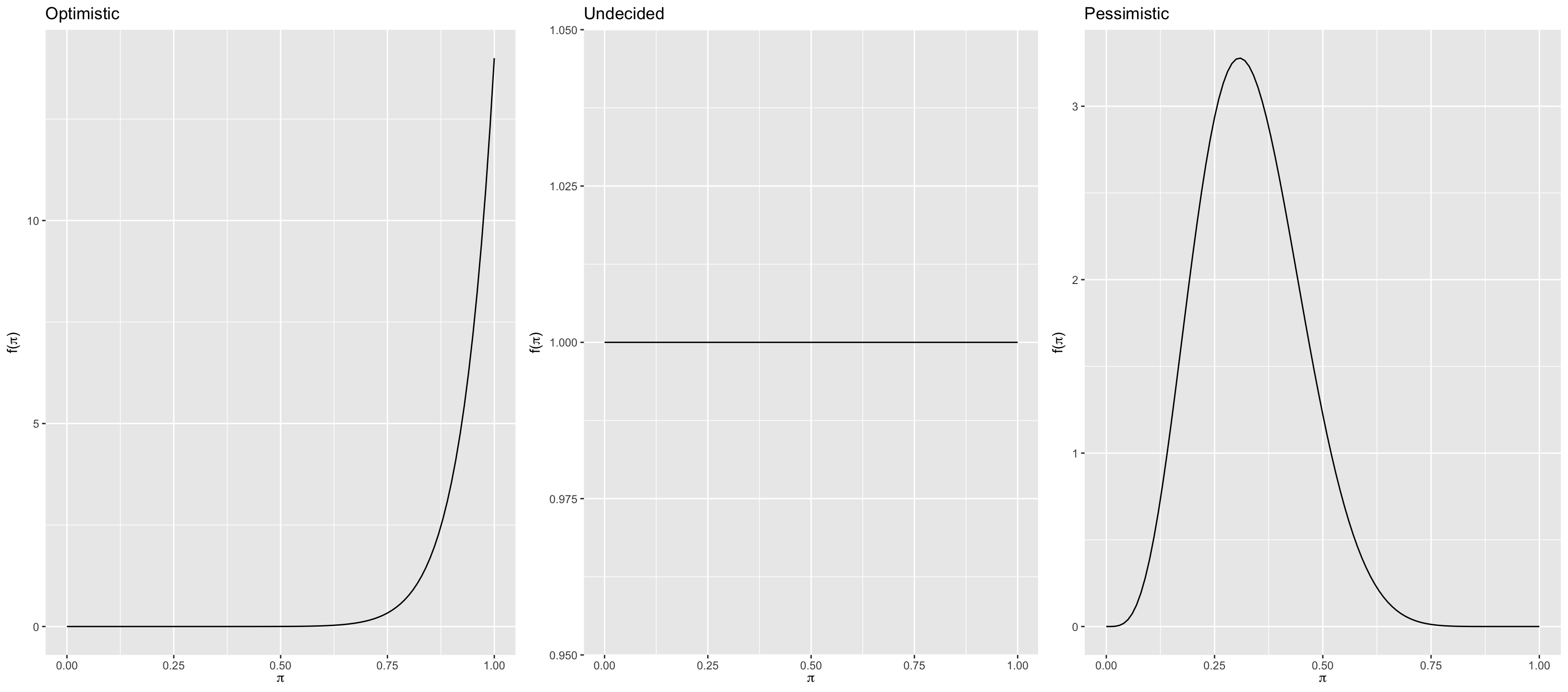
Optimistic	Undecided	Pessimistic
Beta(14, 1)	Beta(1, 1)	Beta(5, 10)

2. Constructing priors

The shape parameters \(\alpha\) and \(\beta\) can be interpreted as the approximate number of successes and failures.

Beta(approx_num_correct, approx_num_wrong).

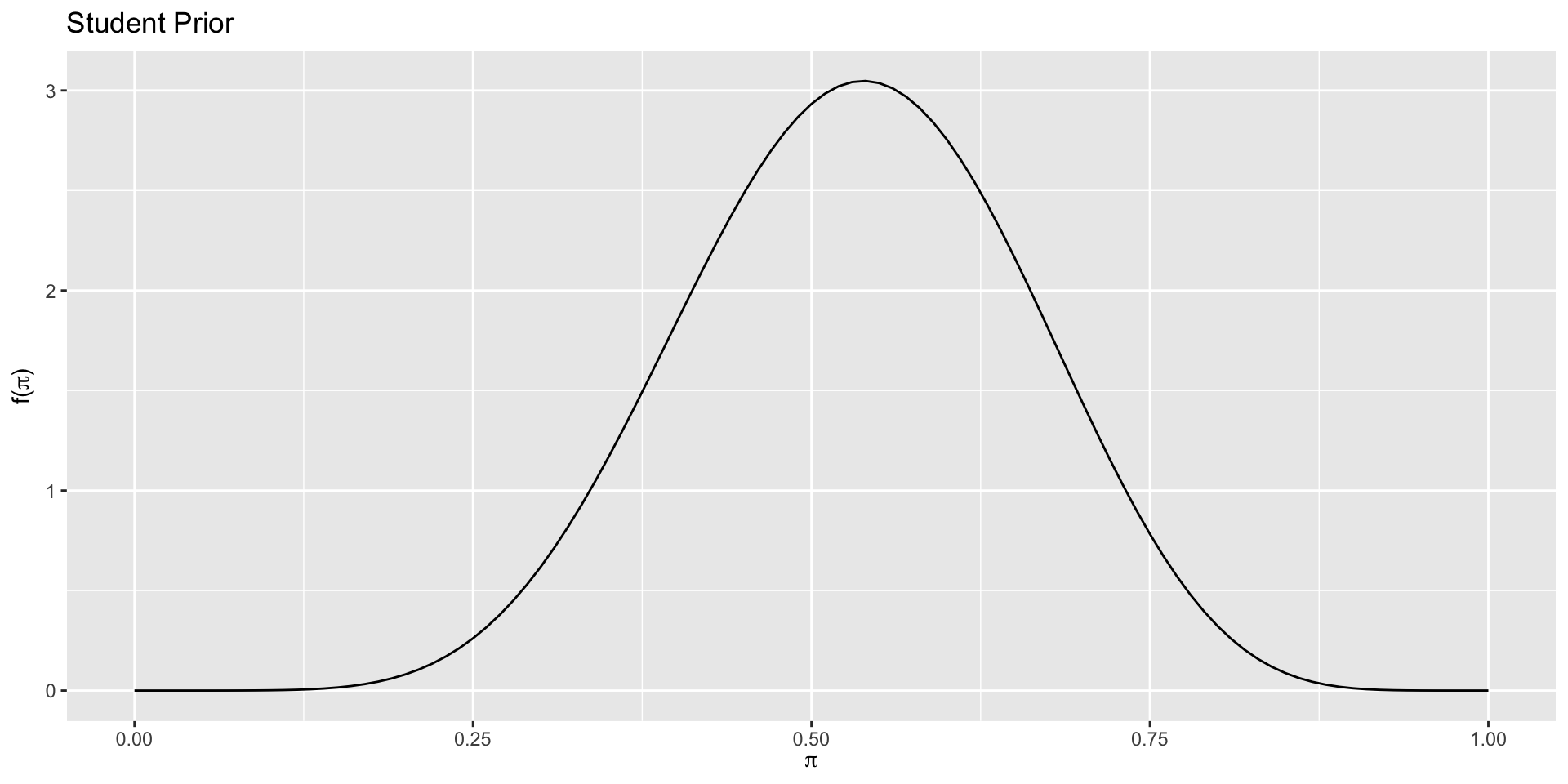
3. Discuss vague vs. informative priors

4. Take the quiz (15 CNN/Onion headlines)

Google Form

5. Update with data

summarize_beta_binomial(alpha, beta, y = NULL, n = NULL) summarizes the mean, mode, and variance of the prior and posterior Beta models of \(\pi\)

plot_beta_binomial(alpha, beta, y = NULL, n = NULL) [function produces a plot of any combination of the corresponding]; plots prior pdf, scaled likelihood function, and posterior pdf

Arguments:

-   `alpha, beta`: positive shape parameters of the prior Beta model
-   `y`: number of successes
-   `n`: number of trials

5. Update with data

summarize_beta_binomial(alpha = 8, beta = 7, y = 10, n = 15)

      model alpha beta      mean      mode         var         sd
1     prior     8    7 0.5333333 0.5384615 0.015555556 0.12472191
2 posterior    18   12 0.6000000 0.6071429 0.007741935 0.08798827

plot_beta_binomial(alpha = 8, beta = 7, y = 10, n = 15)   + 
  labs(title = "Student Prior")

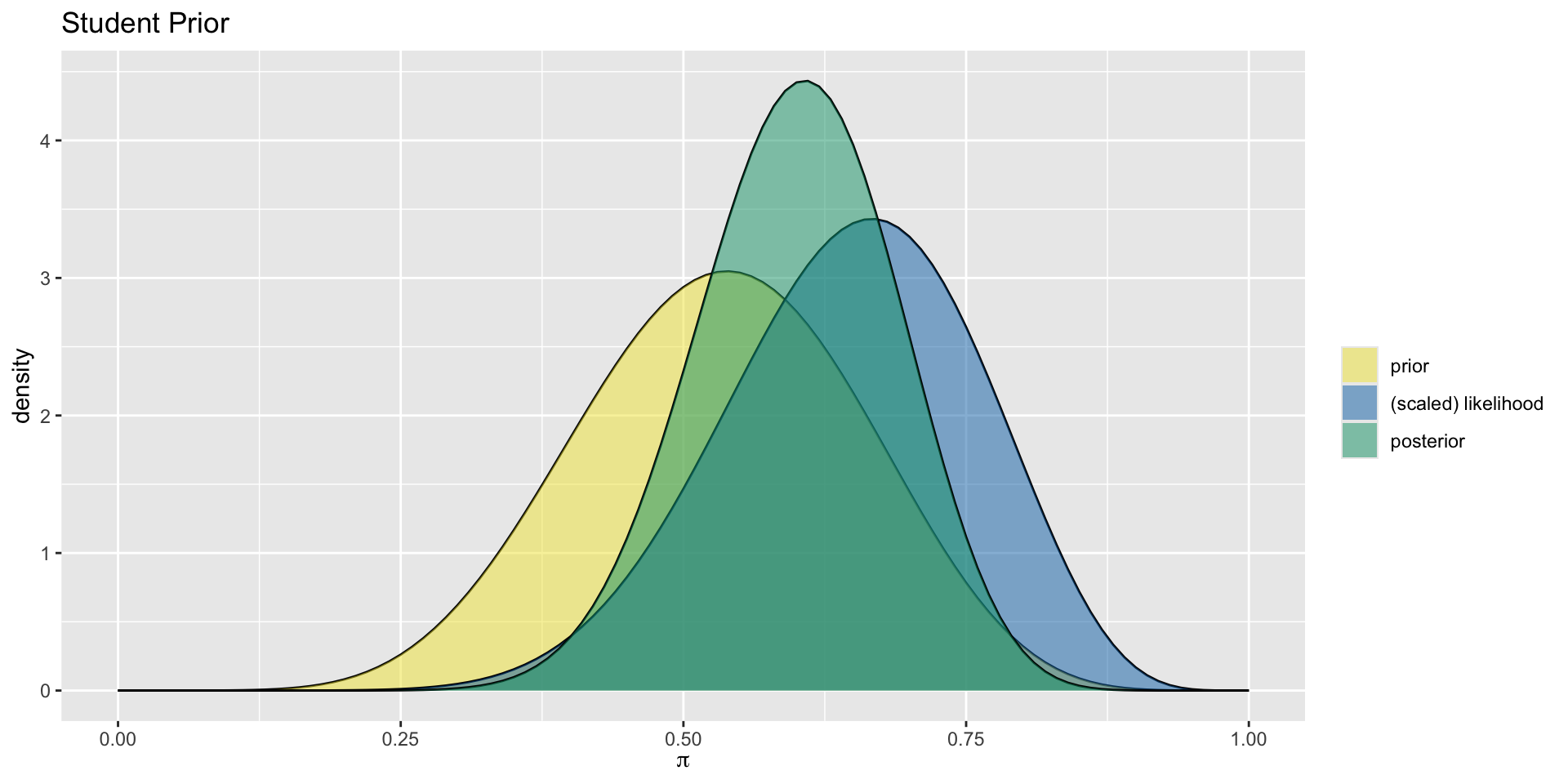
5. Update with data

Optimistic	Undecided	Pessimistic	Student Prior
Beta(14, 1)	Beta(1, 1)	Beta(5, 10)	Beta(8, 7)

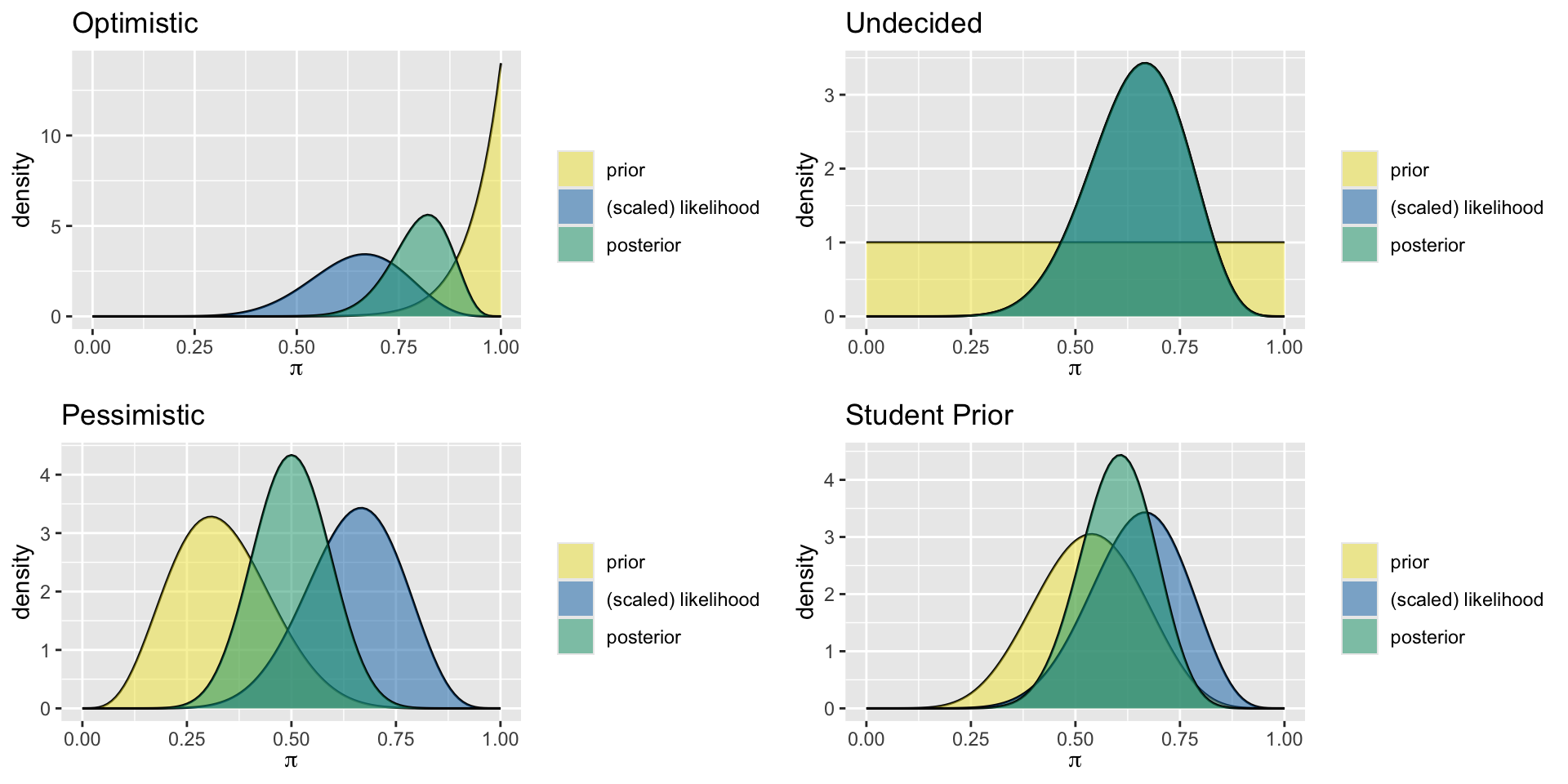
optimistic_prior <- plot_beta_binomial(alpha = 14, beta = 1, y = 10, n = 15) + 
  labs(title = "Optimistic")
undecided_prior <- plot_beta_binomial(alpha = 1, beta = 1, y = 10, n = 15) + 
  labs(title = "Undecided")
pessimistic_prior <- plot_beta_binomial(alpha = 5, beta = 10, y = 10, n = 15) + 
  labs(title = "Pessimistic")
student_prior <- plot_beta_binomial(alpha = 8, beta = 7, y = 10, n = 15)  + 
  labs(title = "Student Prior")

5. Update with data

6. Update with neighbor and class data

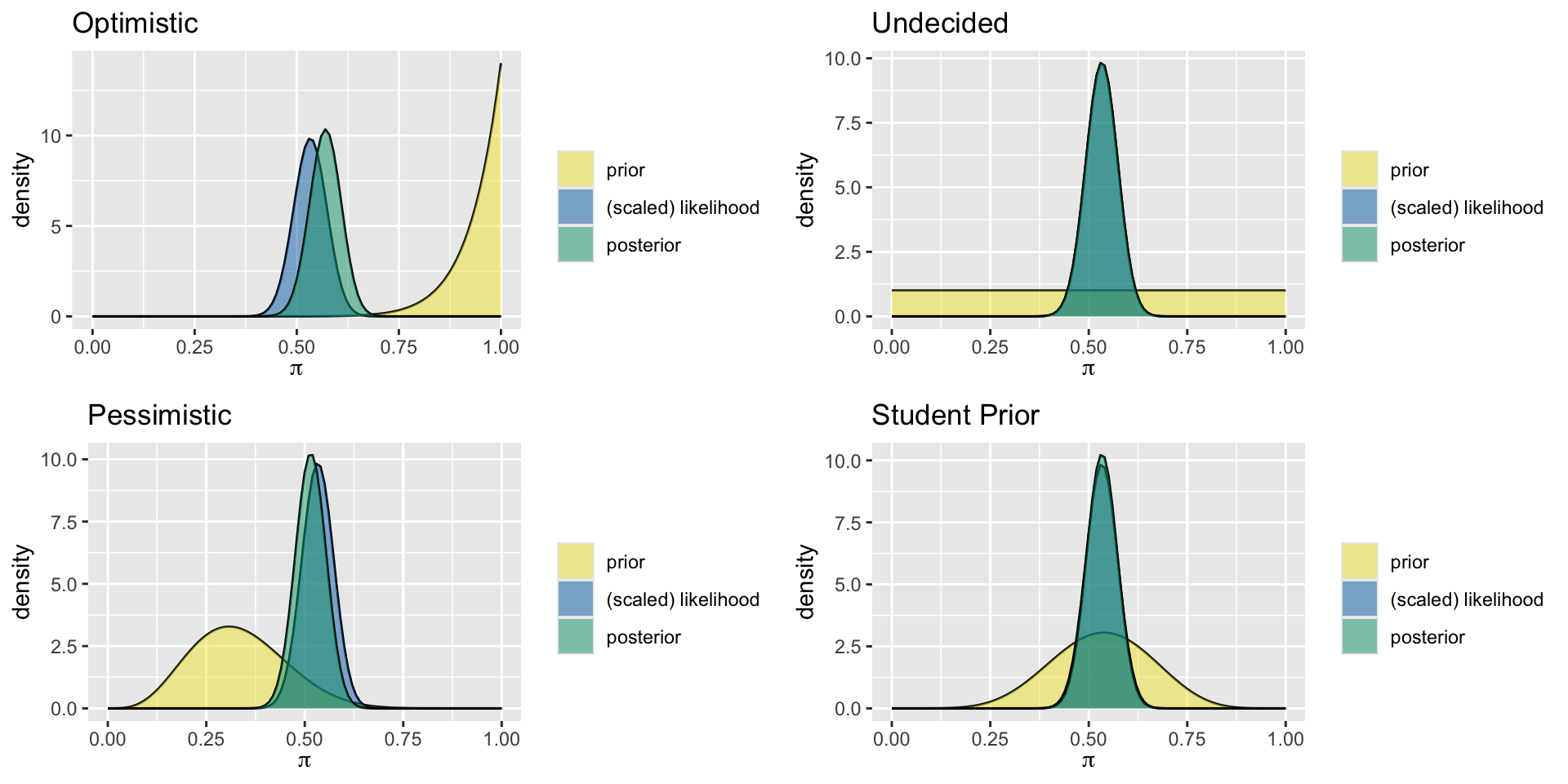
With class data: 80 correct out of 150 questions

Optimistic	Undecided	Pessimistic	Student Prior
Beta(14, 1)	Beta(1, 1)	Beta(5, 10)	Beta(8, 7)

optimist <- plot_beta_binomial(alpha = 14, beta = 1, y = 80, n = 150) + 
  labs(title = "Optimistic")
undecided <- plot_beta_binomial(alpha = 1, beta = 1, y = 80, n = 150) + 
  labs(title = "Undecided")
pessimist <- plot_beta_binomial(alpha = 5, beta = 10, y = 80, n = 150) + 
  labs(title = "Pessimistic")
student_prior <- plot_beta_binomial(alpha = 8, beta = 7, y = 80, n = 150) + 
  labs(title = "Student Prior")

7. Compare effects of prior choice on the posterior

8. Discussion Questions

• How does observing more data affect the shape of the posterior?

• What happens to the posterior mean as you observe more correct or incorrect outcomes?

• In what ways does the posterior reflect a compromise between prior belief and observed data?

Where to find the Activity

Activity Link; Instructor Guide; Github Readme Homepage Link

Conclusions and Next Steps

• Fun activity where students generate their own data and explore Bayesian thinking.
• Plan to gather feedback from students on activity in coming year.
• Make updates based on student and facilitator feedback.
• Adapt activity for different levels of R knowledge.
• Streamline webr experience (missing BayesRule package).

Thanks and Questions

This work was supported by the National Science Foundation under Grant Nos #2215879, #2215920, and #2215709.