Hierarchical Models

Day 5

Note that the example in this lecture is from Chapter 10.2 of Probability and Bayesian Modeling book

Introduction: Observations in Groups

Recap: The Normal Model & Normal Regression

  • When you have continuous outcomes, you can use a normal model: \[\begin{equation*} Y_i \mid \mu, \sigma \overset{i.i.d.}{\sim} \textrm{Normal}(\mu, \sigma^2), \,\,\, i = 1, \cdots, n. \end{equation*}\]

  • When you have predictor variables available, \(\{x_{i1}, \cdots, x_{ip}\}\); you can specify an observation specific mean: \[\begin{equation*} Y_i \mid \mu_i, \sigma \overset{ind}{\sim} \textrm{Normal}(\mu_i, \sigma^2), \,\,\, i = 1, \cdots, n, \text{ where} \end{equation*}\] \[\begin{equation*} \mu_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots, \beta_p x_{ip}. \end{equation*}\]

  • Observations are assumed independent.

When Observations Are Not Necessarily Independent

  • Observations can be dependent in several ways

  • Observations are nested in groups:

    • Students’ test scores from multiple schools
    • Ratings of movies of different genres
    • Death rates of hospitals

Discussion question

Can you think of additional examples of observations in groups?

  • We will focus on a movie rating dataset to explore modeling approaches for dependent data

Example: Ratings of Animation Movies

Ratings of Animation Movies

  • Example from Chapter 10.2 of Probability and Bayesian Modeling book

  • MovieLens: personalized movie recommendation for users

  • In one study, a sample on movie ratings for 8 animation movies released in 2010, total 55 ratings

  • Each rating is for a movie completed by a user; some movies have many ratings while others have few

  • A natural grouping of these 55 ratings: by movie title

Plot of Ratings by Title

library(tidyverse)

MovieRatings <- read.csv("2010_animation_ratings.csv", header = TRUE, sep = ",")

MovieRatings %>%
  mutate(Title = as.character(title),
         Title = recode(Title,
                  "Shrek Forever After (a.k.a. Shrek: The Final Chapter) (2010)" = "Shrek Forever",
                  "How to Train Your Dragon (2010)" = "Dragon",
                  "Toy Story 3 (2010)" = "Toy Story 3",
                  "Tangled (2010)" = "Tangled",
                  "Despicable Me (2010)" = "Despicable Me",
                  "Legend of the Guardians: The Owls of Ga'Hoole (2010)" = "Guardians",
                  "Megamind (2010)" = "Megamind",
                  "Batman: Under the Red Hood (2010)" = "Batman")) ->
           MovieRatings

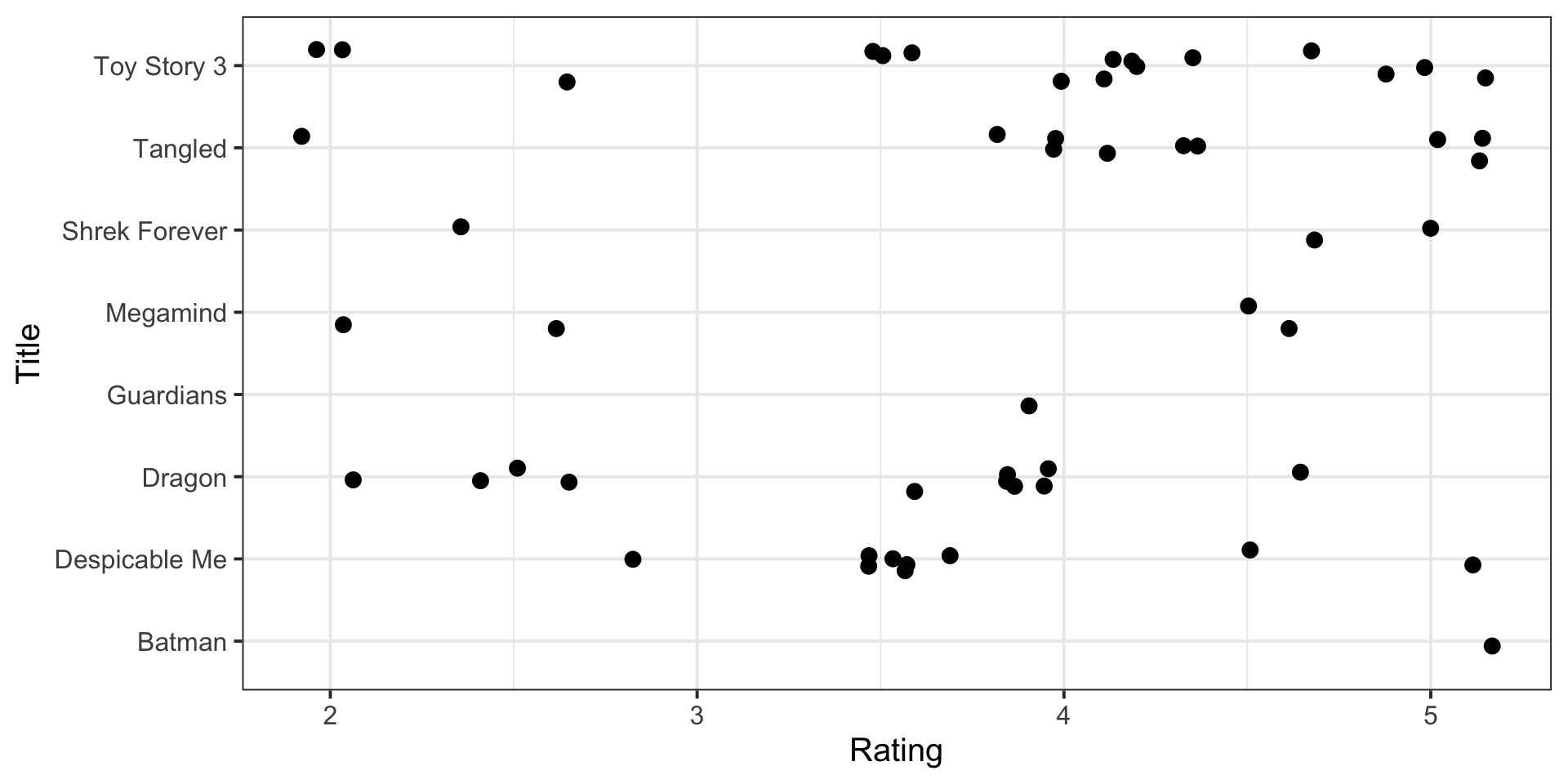
Summary Statistics of Ratings by Title

Movie Title Mean SD N
Batman: Under the Red Hood 5.00 1
Despicable Me 3.72 0.62 9
How to Train Your Dragon 3.41 0.86 11
Legend of the Guardians 4.00 1
Megamind 3.38 1.31 4
Shrek Forever After 4.00 1.32 3
Tangled 4.20 0.89 10
Toy Story 3 3.81 0.96 16

Modeling Challenges

  • Approach 1 - separate estimates for each movie \(j\): \[\begin{equation*} Y_{1j}, \cdots, Y_{n_j j} \overset{i.i.d.}{\sim} \textrm{Normal}(\mu_j, \sigma_j^2) \end{equation*}\]
    • No relation among groups: groups with small sample size might suffer (e.g., \(n_j = 1\))
  • Approach 2 - combined estimates for all \(J\) movies: \[\begin{equation*} Y_{ij} \overset{i.i.d.}{\sim} \textrm{Normal}(\mu, \sigma^2) \end{equation*}\]
    • Differences in groups are ignored

Potential Solutions

  • Something in between - hierarchical/multilevel modeling
    • Pooling information across groups
    • Achieved through a two-stage prior

A Hierarchical Model with Random \(\sigma\)

The Sampling Model

  • Without loss of generality, assume a group-specific normal model for movie \(j\): \[\begin{eqnarray} Y_{ij} \overset{i.i.d.}{\sim} \textrm{Normal}(\mu_j, \sigma^2) \end{eqnarray}\] where \(i = 1, \cdots, n_j\) and \(n_j\) is the number of observations in group \(j\)

  • Model parameters: \(\{\mu_1, \cdots, \mu_J, \sigma\}\)

Discussion question

Is a commonly shared \(\sigma\) reasonable? If not, what can you do?

A Two-Stage Prior for \(\{\mu_1, \cdots, \mu_J\}\): Stage 1

  • All movies are animation movies, we could assume that the mean ratings are similar across movies

  • First stage: the same normal prior distribution for each mean \(\mu_j\) \[\begin{equation} \mu_j \mid \mu, \tau \sim \textrm{Normal}(\mu, \tau^2) \end{equation}\]

  • This prior allows information pooled across movies (groups)

    • If variance is large, the \(\mu_j\)’s are very different a priori \(\rightarrow\) modest pooling in parameter estimation
    • If variance is small, the \(\mu_j\)’s are very similar a priori \(\rightarrow\) large pooling in parameter estimation

  • \(\mu\) and \(\tau\): hyperparameters, and treated random

A Two-Stage Prior for \(\{\mu_1, \cdots, \mu_J\}\): Stage 2

  • Second stage: weakly informative hyperpriors for hyperparameters \[\begin{eqnarray} \mu &\sim& \textrm{Normal}(3, 1) \\ \tau &\sim& \textrm{Cauchy}(0, 1) \end{eqnarray}\]

  • After posterior inference:

    • The posterior of \(\mu\) is informative about an average mean rating
    • The posterior of \(\tau\) is informative about the variation among the \(\mu_j\)

Prior for \(\sigma\) and Graphical Representation

  • Weakly informative prior for \(\sigma\): \[\begin{eqnarray} \sigma &\sim& \textrm{Cauchy}(0, 1) \end{eqnarray}\]

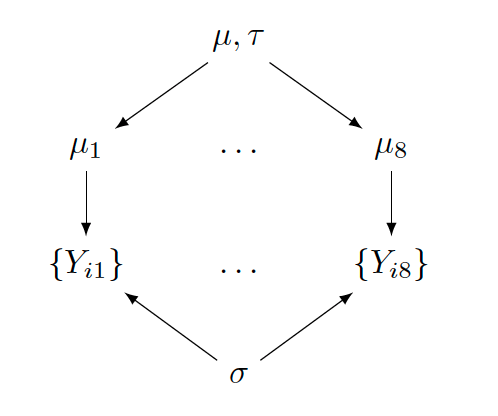
Discussion question

Describe how the graphical representation corresponds to the hierarchical model. What parameters/hyperparameters are shared among what?

MCMC Estimation and Diagnostics

Fitting The Model

  • Use the brm() function with family = gaussian

  • Use rating ~ 1 + (1 | Title) expression for model specification

library(brms)
ml_fit <- brm(data = MovieRatings, family = gaussian,
               rating ~ 1 + (1 | Title),
               prior = c(prior(normal(3, 1), class = Intercept),
                         prior(cauchy(0, 1), class = sd),
                         prior(cauchy(0, 1), class = sigma)),
               iter = 20000, warmup = 10000, thin = 10, chains = 2, 
               seed = 123)

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 4.7e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.47 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:     1 / 20000 [  0%]  (Warmup)
Chain 1: Iteration:  2000 / 20000 [ 10%]  (Warmup)
Chain 1: Iteration:  4000 / 20000 [ 20%]  (Warmup)
Chain 1: Iteration:  6000 / 20000 [ 30%]  (Warmup)
Chain 1: Iteration:  8000 / 20000 [ 40%]  (Warmup)
Chain 1: Iteration: 10000 / 20000 [ 50%]  (Warmup)
Chain 1: Iteration: 10001 / 20000 [ 50%]  (Sampling)
Chain 1: Iteration: 12000 / 20000 [ 60%]  (Sampling)
Chain 1: Iteration: 14000 / 20000 [ 70%]  (Sampling)
Chain 1: Iteration: 16000 / 20000 [ 80%]  (Sampling)
Chain 1: Iteration: 18000 / 20000 [ 90%]  (Sampling)
Chain 1: Iteration: 20000 / 20000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.397 seconds (Warm-up)
Chain 1:                0.432 seconds (Sampling)
Chain 1:                0.829 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 6e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:     1 / 20000 [  0%]  (Warmup)
Chain 2: Iteration:  2000 / 20000 [ 10%]  (Warmup)
Chain 2: Iteration:  4000 / 20000 [ 20%]  (Warmup)
Chain 2: Iteration:  6000 / 20000 [ 30%]  (Warmup)
Chain 2: Iteration:  8000 / 20000 [ 40%]  (Warmup)
Chain 2: Iteration: 10000 / 20000 [ 50%]  (Warmup)
Chain 2: Iteration: 10001 / 20000 [ 50%]  (Sampling)
Chain 2: Iteration: 12000 / 20000 [ 60%]  (Sampling)
Chain 2: Iteration: 14000 / 20000 [ 70%]  (Sampling)
Chain 2: Iteration: 16000 / 20000 [ 80%]  (Sampling)
Chain 2: Iteration: 18000 / 20000 [ 90%]  (Sampling)
Chain 2: Iteration: 20000 / 20000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.401 seconds (Warm-up)
Chain 2:                0.411 seconds (Sampling)
Chain 2:                0.812 seconds (Total)
Chain 2:

Fitting The Model Exercise

Discussion question

Can you come up with stan_glm() from the rstanarm R package to fit this model?

Saving Posterior Draws

  • Save post as a matrix of simulated posterior draws

  • The model parameters: \(\{\mu, \tau, \mu_1, \cdots, \mu_8, \sigma\}\)

post_ml <- as_draws_df(ml_fit)
print(post_ml)
# A draws_df: 1000 iterations, 2 chains, and 14 variables
   b_Intercept sd_Title__Intercept sigma Intercept r_Title[Batman,Intercept]
1          3.8               0.173  0.78       3.8                     0.352
2          3.9               0.253  0.79       3.9                     0.486
3          3.9               0.164  1.02       3.9                     0.209
4          4.0               0.316  1.00       4.0                     0.258
5          3.8               0.407  1.03       3.8                    -0.140
6          3.7               0.134  0.98       3.7                    -0.219
7          3.7               0.233  0.94       3.7                    -0.050
8          3.9               0.203  0.95       3.9                     0.413
9          3.6               0.324  0.83       3.6                     0.573
10         3.8               0.068  0.92       3.8                     0.042
   r_Title[Despicable.Me,Intercept] r_Title[Dragon,Intercept]
1                           -0.1392                   -0.0858
2                           -0.2389                   -0.1727
3                            0.0120                   -0.0624
4                           -0.2161                   -0.4593
5                            0.1898                   -0.1110
6                           -0.1307                   -0.2995
7                            0.1033                   -0.5072
8                           -0.2309                    0.0104
9                            0.0286                    0.3298
10                          -0.0036                    0.0019
   r_Title[Guardians,Intercept]
1                         0.121
2                        -0.140
3                        -0.024
4                         0.034
5                        -0.486
6                         0.165
7                         0.097
8                        -0.089
9                         1.006
10                       -0.069
# ... with 1990 more draws, and 6 more variables
# ... hidden reserved variables {'.chain', '.iteration', '.draw'}

Posterior Plots

  • Function mcmc_areas() displays a density estimate of the simulated posterior draws with a specified credible interval
library(bayesplot)
mcmc_areas(post_ml, 
           pars = c("b_Intercept", "r_Title[Batman,Intercept]"), 
           prob = 0.95)

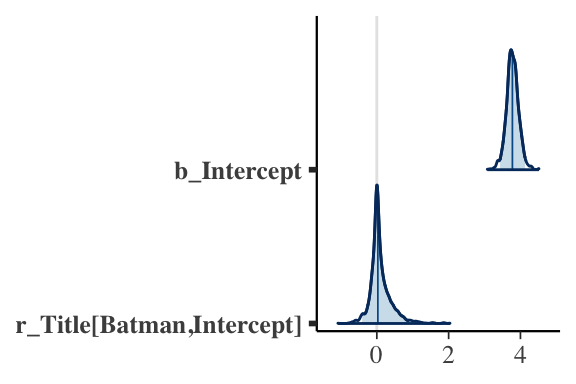
Posterior Plots

library(bayesplot)
mcmc_areas(post_ml, 
           pars = c("b_Intercept", 
                    "r_Title[Batman,Intercept]", 
                    "r_Title[Despicable.Me,Intercept]", 
                    "r_Title[Dragon,Intercept]",
                    "r_Title[Guardians,Intercept]",
                    "r_Title[Megamind,Intercept]",
                    "r_Title[Shrek.Forever,Intercept]",
                    "r_Title[Tangled,Intercept]",
                    "r_Title[Toy.Story.3,Intercept]"), 
           prob = 0.95)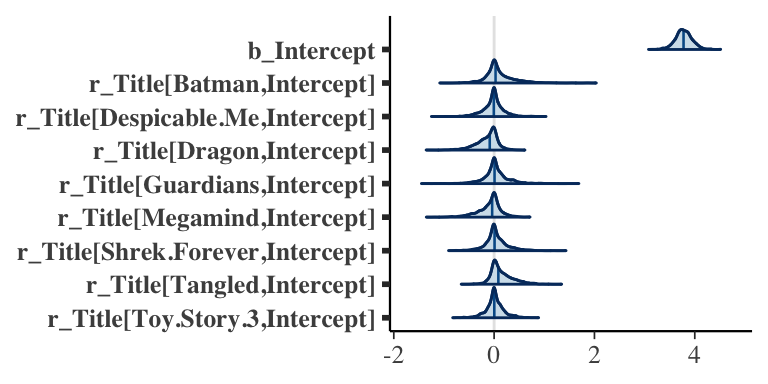

Posterior Plots

  • Between-group variability \(\tau\) vs within-group variability \(\sigma\)
library(bayesplot)
mcmc_areas(post_ml, 
           pars = c("sd_Title__Intercept", "sigma"), 
           prob = 0.95)

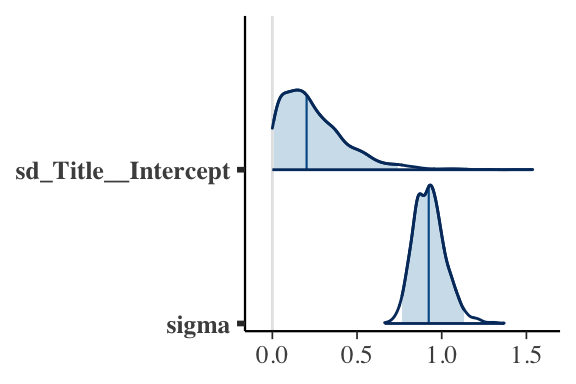
MCMC Diagnostics

ml_fit <- brm(data = MovieRatings, family = gaussian,
               rating ~ 1 + (1 | Title),
               prior = c(prior(normal(3, 1), class = Intercept),
                         prior(cauchy(0, 1), class = sd),
                         prior(cauchy(0, 1), class = sigma)),
               iter = 20000, warmup = 10000, thin = 10, chains = 2, 
               seed = 1234)
  • iter: total number of iterations
  • warmup: the number of iterations to be discarded (beginning iterations are not converged)
  • thin: the number of draws to thin for saving
  • chains: the number of MCMC chains (some diagnostics can only be done for more than one chain)

MCMC Diagnostics: Traceplot

  • Function mcmc_trace() displays a traceplot of the simulated posterior draws for each chain

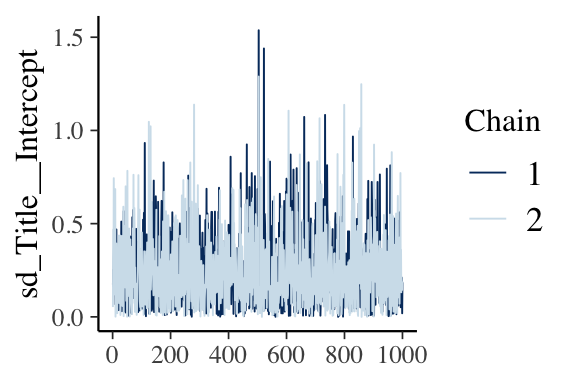
MCMC Diagnostics: Autocorrelation Plot

  • Function mcmc_acf() displays an autocorrelation plot of the simulated posterior draws

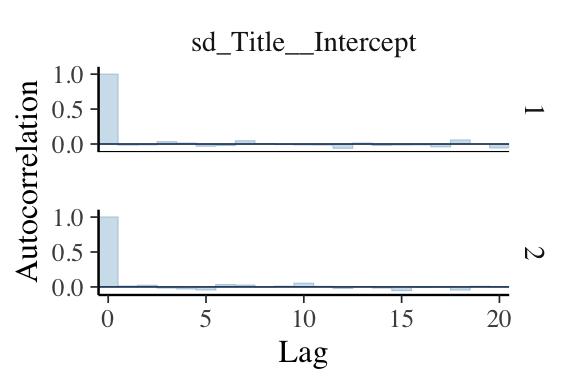
Additional Bayesian Inferential Questions

Shrinkage/Pooling Effects

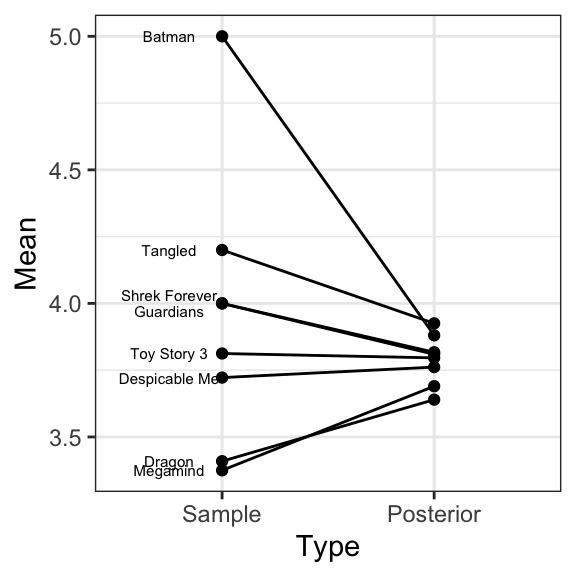
Sources of Variability

  • Two sources of variability in \(Y_{ij}\): \[\begin{eqnarray*} Y_{ij} &\overset{i.i.d.}{\sim}& \textrm{Normal}(\mu_j, \sigma^2) \,\,\, \text{[within-group variability]} \\ \mu_j &\sim& \textrm{Normal}(\mu, \tau^2) \,\,\, \text{[between-group variability]} \end{eqnarray*}\]

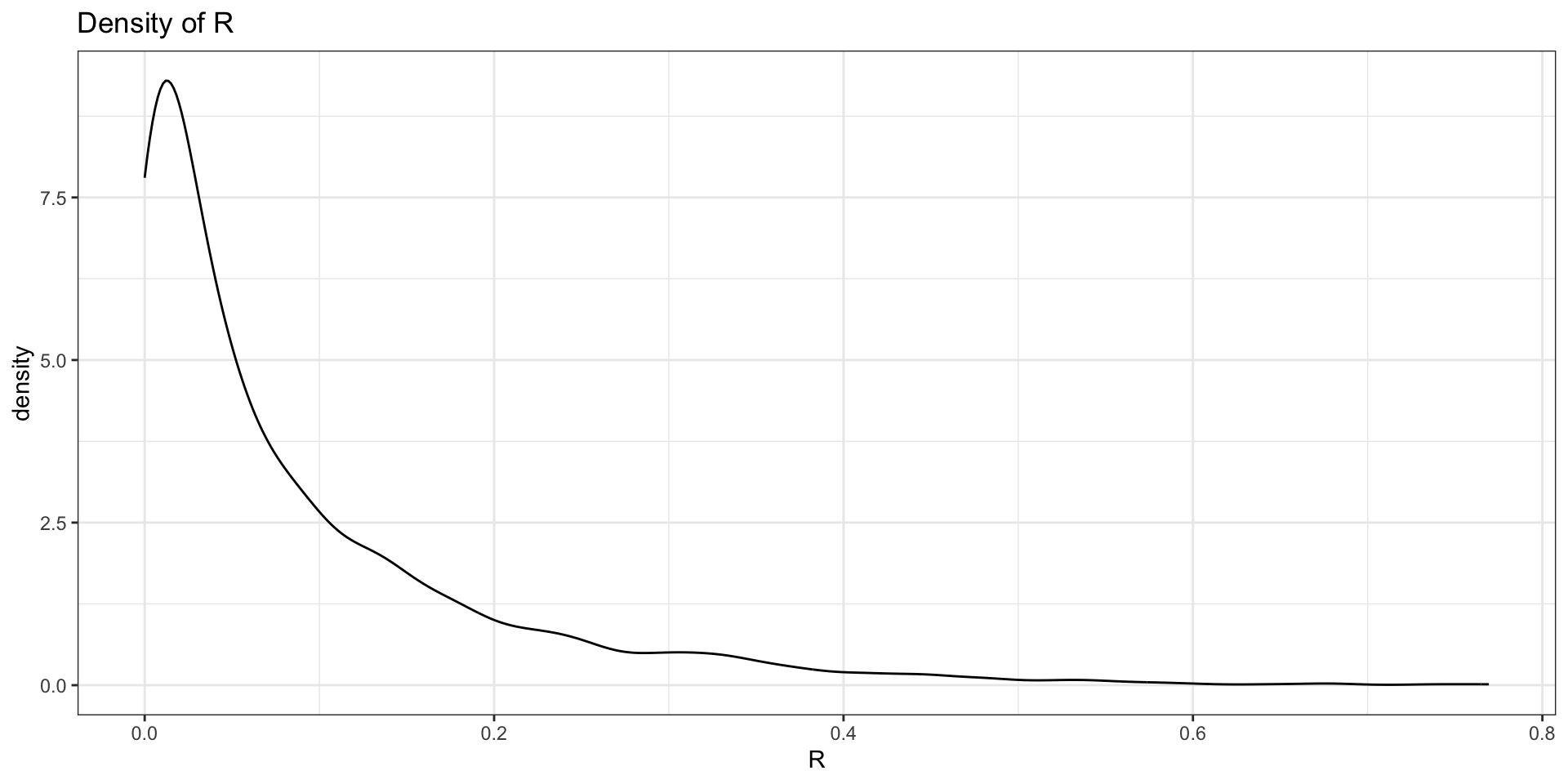
  • To compare these two sources of variability, one can compute the fraction \[\begin{equation*} R = \frac{\tau^2}{\tau^2 + \sigma^2} \end{equation*}\] from the posterior draws of \(\tau\) and \(\sigma\)

  • If \(R \rightarrow 1\), the higher the between-group variability

Sources of Variability: Results

tau_draws <- post_ml$sd_Title__Intercept
sigma_draws <- post_ml$sigma
R <- tau_draws^2/(tau_draws^2 + sigma_draws^2)
quantile(R, c(0.025, 0.975))
        2.5%        97.5% 
8.950522e-05 3.946648e-01