Evaluating
regression models

Day 4

Note that examples in this part of the lecture are a simplified version of Chapter 10 of Bayes Rules! book.

Packages

library(bayesrules)
library(tidyverse)
library(rstanarm)
library(bayesplot)

  1. How fair is the model? How was the data collected? By whom and for what purpose? How might the results of the analysis, or the data collection itself, impact individuals and society? What biases or power structures might be baked into this analysis?

  2. How wrong is the model? George Box famously said: “All models are wrong, but some are useful.” What’s important to know then is, how wrong is our model? Are our model assumptions reasonable?

  3. How accurate are the posterior predictive models?

Checking Model Assumptions

\[Y_i | \beta_0, \beta_1, \sigma \stackrel{ind}{\sim} N(\mu_i, \sigma^2) \;\; \text{ with } \;\; \mu_i = \beta_0 + \beta_1 X_i .\]

  1. Conditioned on \(X\), the observed data \(Y_i\) on case \(i\) is independent of the observed data on any other case \(j\).
  2. The typical \(Y\) outcome can be written as a linear function of \(X\), \(\mu = \beta_0 + \beta_1 X\).
  3. At any \(X\) value, \(Y\) varies normally around \(\mu\) with consistent variability \(\sigma\).

Independence

When taken alone, ridership \(Y\) is likely correlated over time – today’s ridership likely tells us something about tomorrow’s ridership. Yet much of this correlation, or dependence, can be explained by the time of year and features associated with the time of year – like temperature \(X\). Thus, knowing the temperature on two subsequent days may very well “cancel out” the time correlation in their ridership data.

Linearity and Constant Variance

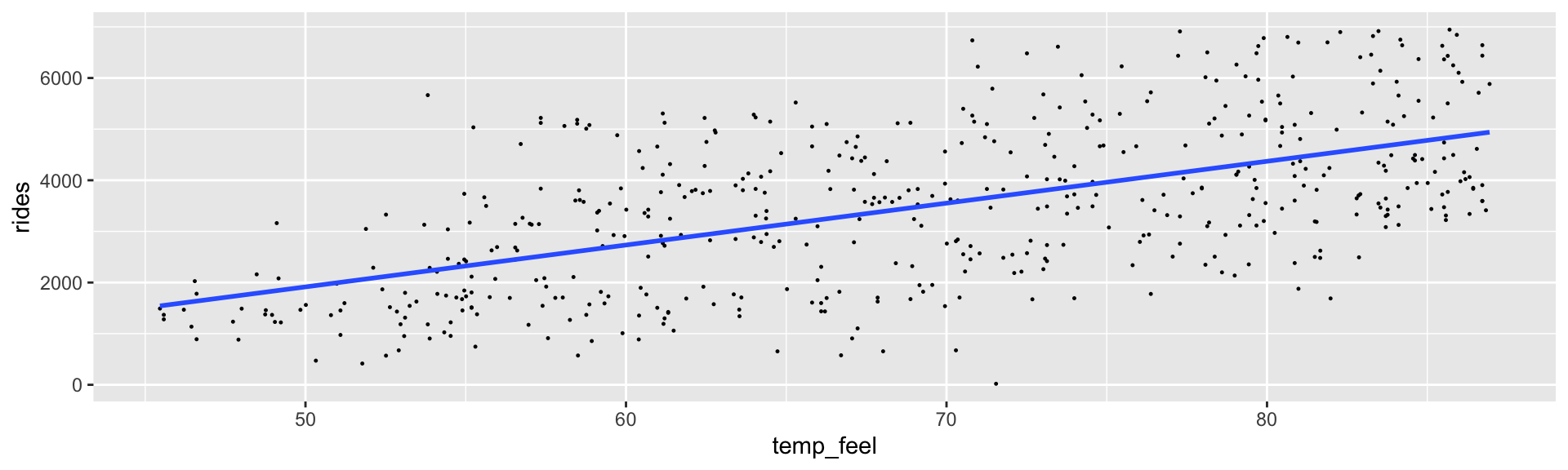
The relationship between ridership and temperature does appear to be linear. Further, with the slight exception of colder days on which ridership is uniformly small, the variability in ridership does appear to be roughly consistent across the range of temperatures \(X\).

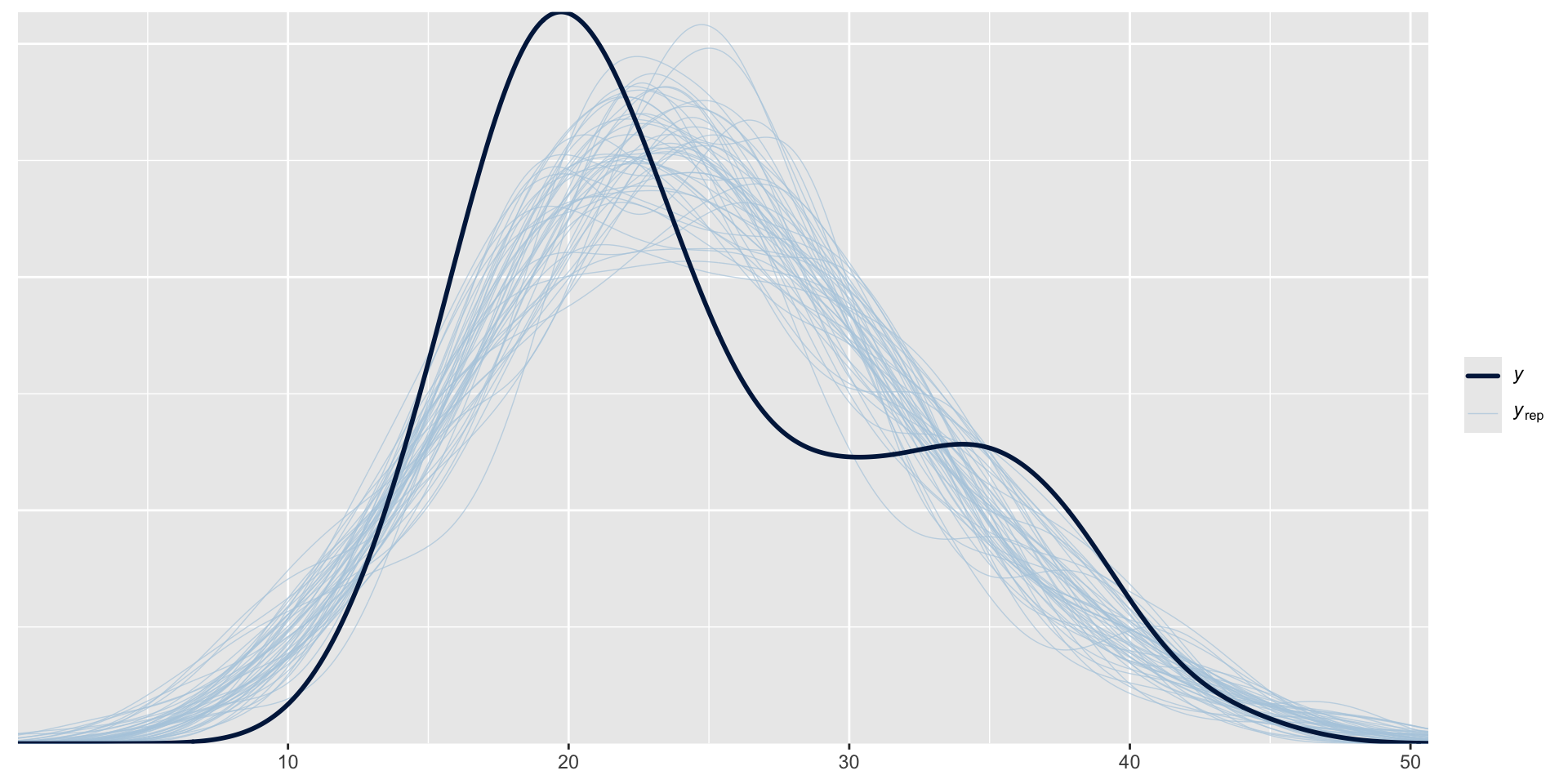
Posterior predictive check

Consider a regression model with response variable \(Y\), predictor \(X\), and a set of regression parameters \(\theta\). For example, in the model in the previous slides \(\theta = (\beta_0,\beta_1,\sigma)\). Further, let \(\left\lbrace \theta^{(1)}, \theta^{(2)}, \ldots, \theta^{(N)}\right\rbrace\) be an \(N\)-length Markov chain for the posterior model of \(\theta\). Then a “good” Bayesian model will produce predictions of \(Y\) with features similar to the original \(Y\) data. To evaluate whether your model satisfies this goal:

  1. At each set of posterior plausible parameters \(\theta^{(i)}\), simulate a sample of \(Y\) values from the likelihood model, one corresponding to each \(X\) in the original sample of size \(n\). This produces \(N\) separate samples of size \(n\).
  2. Compare the features of the \(N\) simulated \(Y\) samples, or a subset of these samples, to those of the original \(Y\) data.

bike_model <- stan_glm(rides ~ temp_feel, data = bikes,
                       family = gaussian,
                       prior_intercept = normal(5000, 1000),
                       prior = normal(100, 40), 
                       prior_aux = exponential(0.0008),
                       chains = 4, iter = 5000*2, seed = 84735, refresh = FALSE)
bike_model_df <- as.data.frame(bike_model)

first_set <- head(bike_model_df, 1)
beta_0 <- first_set$`(Intercept)`
beta_1 <- first_set$temp_feel
sigma  <- first_set$sigma
set.seed(84735)
one_simulation <- bikes %>% 
  mutate(mu = beta_0 + beta_1 * temp_feel,
         simulated_rides = rnorm(500, mean = mu, sd = sigma)) %>% 
  select(temp_feel, rides, simulated_rides)

head(one_simulation, 2)
  temp_feel rides simulated_rides
1  64.72625   654        3962.406
2  49.04645  1229        1657.900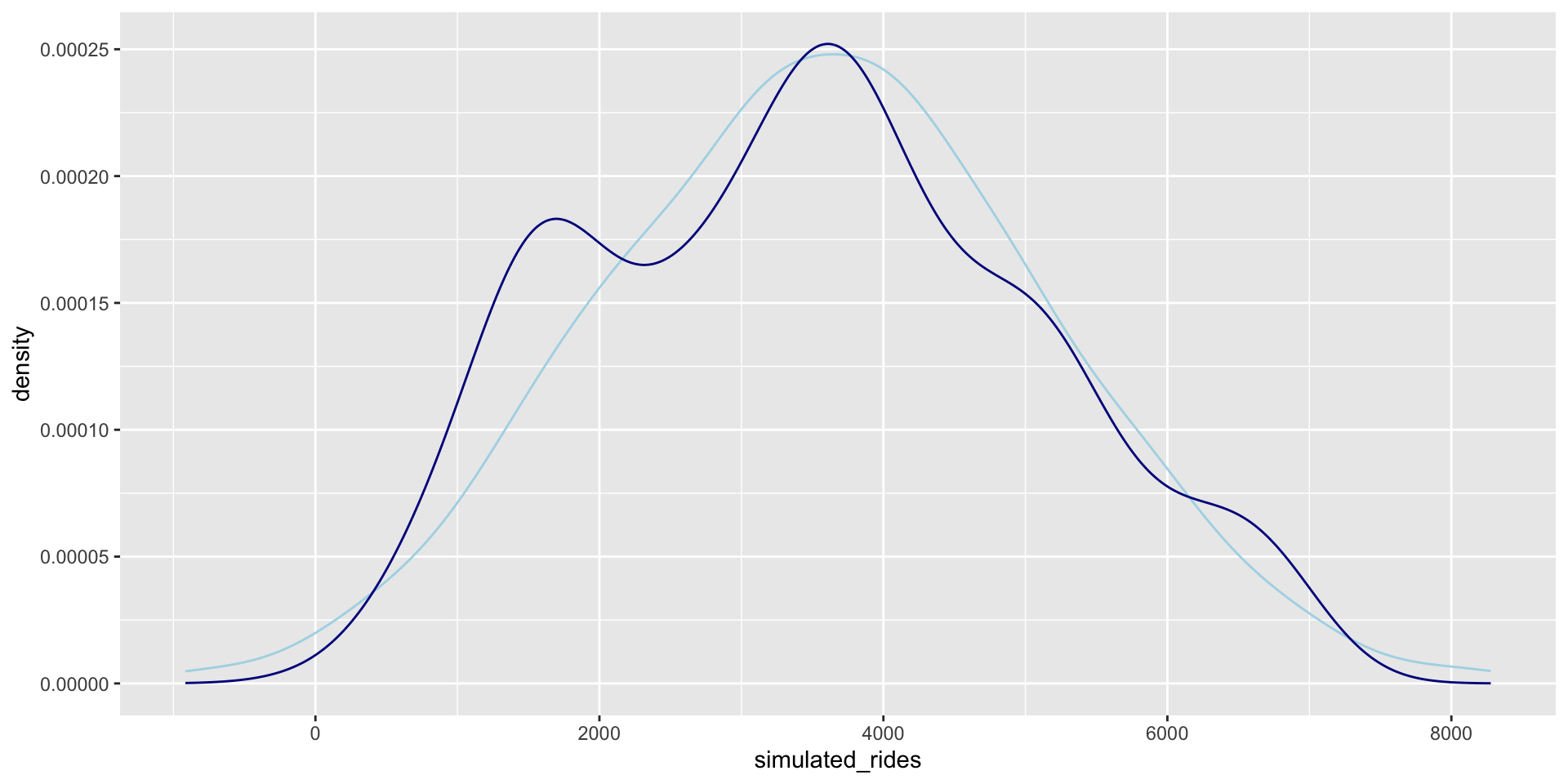

ggplot(one_simulation, aes(x = simulated_rides)) + 
  geom_density(color = "lightblue") + 
  geom_density(aes(x = rides), color = "darkblue")

One posterior simulated dataset of ridership (light blue) along with the actual observed ridership data (dark blue)

# Examine 50 of the 20000 simulated samples
pp_check(bike_model, nreps = 50) + 
  xlab("rides")

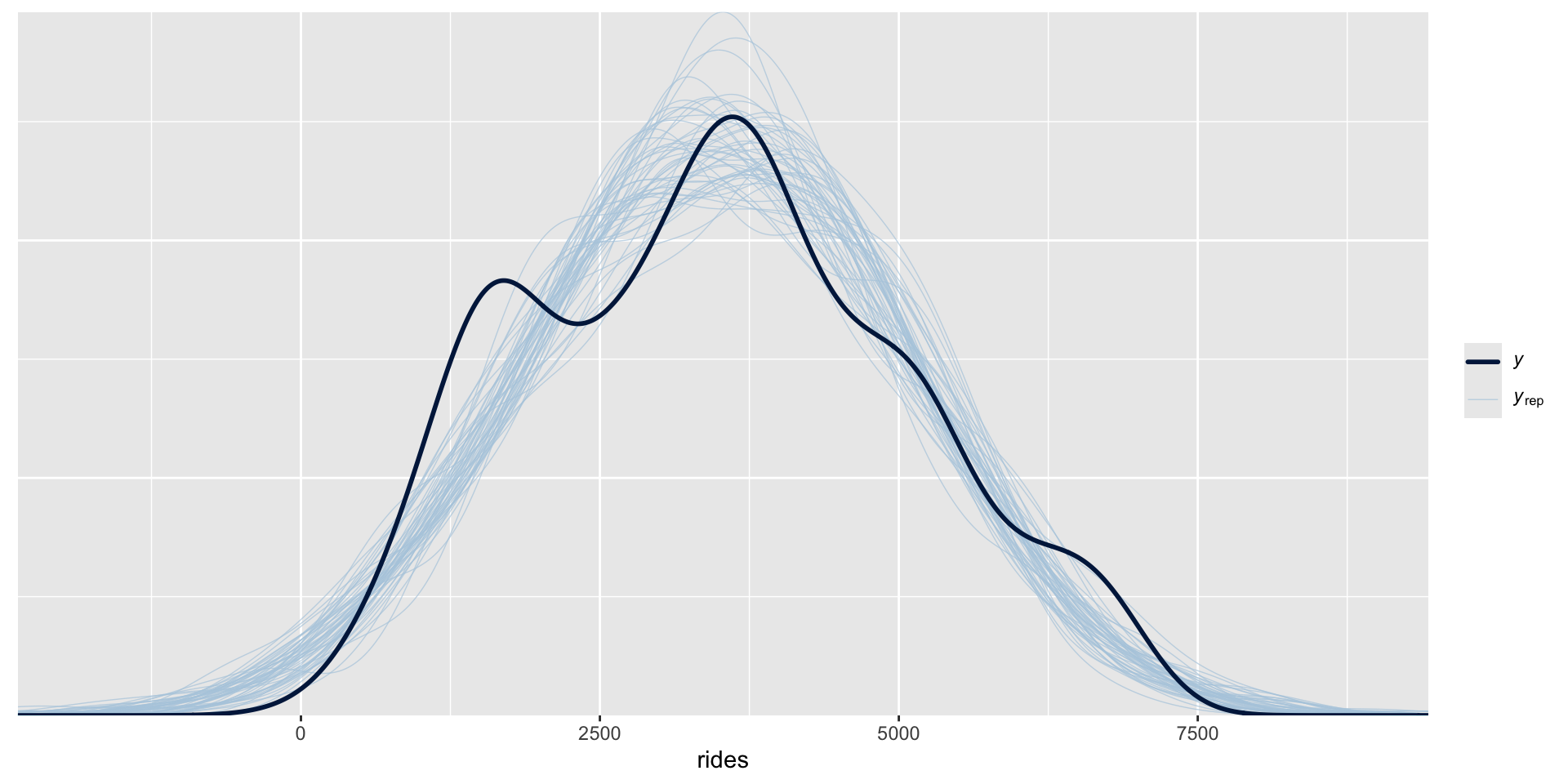
How accurate are the posterior predictive models?

bikes %>% 
  filter(date == "2012-10-22") %>% 
  select(temp_feel, rides)
  temp_feel rides
1  75.46478  6228
set.seed(84735)
predict_75 <- bike_model_df %>% 
  mutate(mu = `(Intercept)` + temp_feel*75) %>% 
  mutate(y_new = rnorm(20000, mu, sigma))

predict_75 %>% 
  summarize(mean = mean(y_new), error = 6228 - mean(y_new))
      mean    error
1 3965.948 2262.052

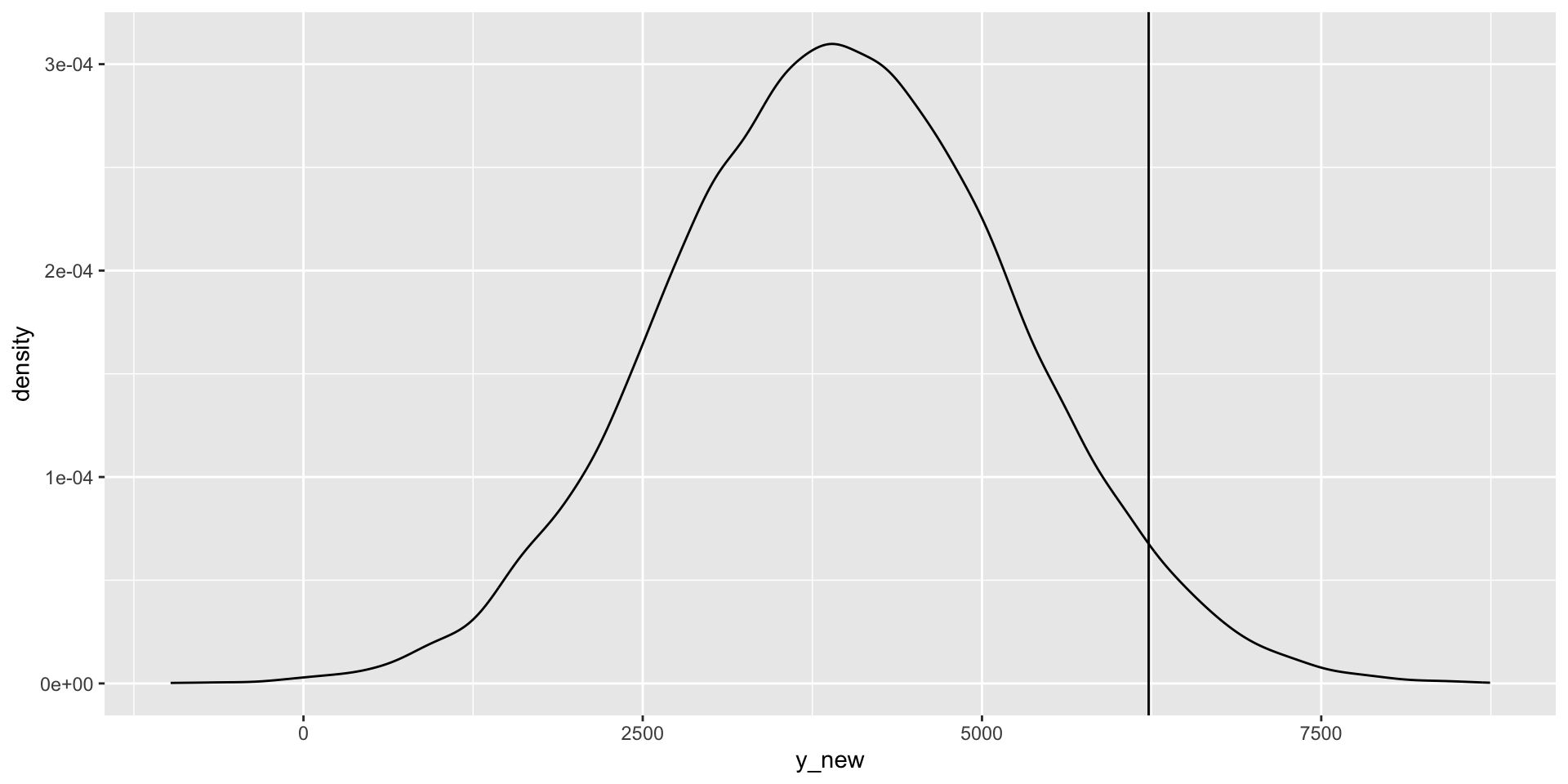
observed value: \(Y\)
posterior predictive mean: \(Y'\)
predictive error: \(Y - Y'\)

predict_75 %>% 
  summarize(mean = mean(y_new), error = 6228 - mean(y_new))
      mean    error
1 3965.948 2262.052

predict_75 %>% 
  summarize(sd = sd(y_new), error = 6228 - mean(y_new),
            error_scaled = error / sd(y_new))
        sd    error error_scaled
1 1280.641 2262.052     1.766343

predict_75 %>% 
  summarize(lower_95 = quantile(y_new, 0.025),
            lower_50 = quantile(y_new, 0.25),
            upper_50 = quantile(y_new, 0.75),
            upper_95 = quantile(y_new, 0.975))
  lower_95 lower_50 upper_50 upper_95
1 1505.486  3091.82 4825.569 6500.895

set.seed(84735)
predictions <- posterior_predict(bike_model, newdata = bikes)

dim(predictions)
[1] 20000   500

ppc_intervals(bikes$rides, yrep = predictions, x = bikes$temp_feel, 
              prob = 0.5, prob_outer = 0.95)

Let \(Y_1, Y_2, \ldots, Y_n\) denote \(n\) observed outcomes. Then each \(Y_i\) has a corresponding posterior predictive model with mean \(Y_i'\) and standard deviation \(\text{sd}_i\). We can evaluate the overall posterior predictive model quality by the following measures:

  • mae
    The median absolute error (MAE) measures the typical difference between the observed \(Y_i\) and their posterior predictive means \(Y_i'\),

    \[\text{MAE} = \text{median}|Y_i - Y_i'|.\]

  • mae_scaled
    The scaled median absolute error measures the typical number of standard deviations that the observed \(Y_i\) fall from their posterior predictive means \(Y_i'\):

    \[\text{MAE scaled} = \text{median}\frac{|Y_i - Y_i'|}{\text{sd}_i}.\]

  • within_50 and within_95
    The within_50 statistic measures the proportion of observed values \(Y_i\) that fall within their 50% posterior prediction interval. The within_95 statistic is similar, but for 95% posterior prediction intervals.

# Posterior predictive summaries
prediction_summary(bike_model, data = bikes)
       mae mae_scaled within_50 within_95
1 981.4852  0.7662329     0.432     0.966

The k-fold cross validation algorithm

  1. Create folds. Let \(k\) be some integer from 2 to our original sample size \(n\). Split the data into \(k\) folds, or subsets, of roughly equal size.

  2. Train and test the model.

    • Train the model using the first \(k - 1\) data folds combined.
    • Test this model on the \(k\)th data fold.
    • Measure the prediction quality (eg: by MAE).

  3. Repeat. Repeat step 2 \(k - 1\) times, each time leaving out a different fold for testing.

  4. Calculate cross-validation estimates. Steps 2 and 3 produce \(k\) different training models and \(k\) corresponding measures of prediction quality. Average these \(k\) measures to obtain a single cross-validation estimate of prediction quality.

set.seed(84735)
cv_procedure <- prediction_summary_cv(
  data = bikes, model = bike_model, k = 10)

cv_procedure$folds
   fold       mae mae_scaled within_50 within_95
1     1  989.7762  0.7695030      0.46      0.98
2     2  965.8257  0.7437664      0.42      1.00
3     3  950.1749  0.7293460      0.42      0.98
4     4 1018.4675  0.7910048      0.46      0.98
5     5 1161.8823  0.9095826      0.36      0.96
6     6  937.5788  0.7328797      0.46      0.94
7     7 1270.1276  1.0058929      0.32      0.96
8     8 1112.5668  0.8604929      0.36      1.00
9     9 1099.2077  0.8677931      0.40      0.92
10   10  786.7470  0.6057405      0.56      0.96

cv_procedure$cv
       mae mae_scaled within_50 within_95
1 1029.235  0.8016002     0.422     0.968

Note that examples in this part of the lecture are a simplified version of Chapter 11 of Bayes Rules! book.

Data

weather_WU <- weather_australia %>% 
  filter(location %in% c("Wollongong", "Uluru")) %>%
  mutate(location = droplevels(as.factor(location))) %>% 
  select(location, windspeed9am, humidity9am, 
    pressure9am, temp9am, temp3pm)
glimpse(weather_WU)
Rows: 200
Columns: 6
$ location     <fct> Uluru, Uluru, Uluru, Uluru, Uluru, Uluru, Uluru, Uluru, U…
$ windspeed9am <dbl> 20, 9, 7, 28, 24, 22, 22, 4, 2, 9, 20, 20, 9, 22, 9, 24, …
$ humidity9am  <int> 23, 71, 15, 29, 10, 32, 43, 57, 64, 40, 28, 30, 95, 47, 7…
$ pressure9am  <dbl> 1023.3, 1012.9, 1012.3, 1016.0, 1010.5, 1012.2, 1025.7, 1…
$ temp9am      <dbl> 20.9, 23.4, 24.1, 26.4, 36.7, 25.1, 14.9, 15.9, 24.6, 15.…
$ temp3pm      <dbl> 29.7, 33.9, 39.7, 34.2, 43.3, 33.5, 24.0, 22.6, 33.2, 24.…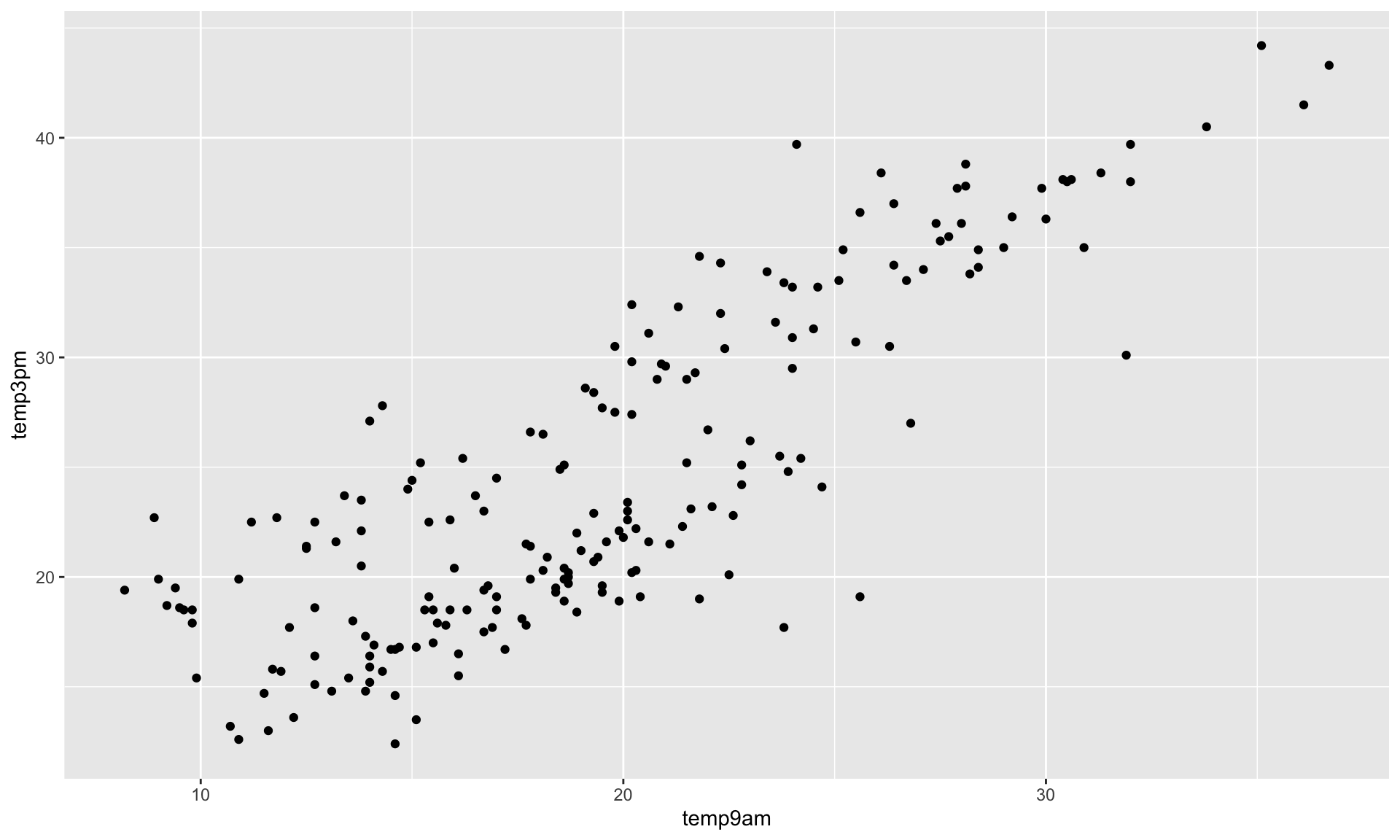

ggplot(weather_WU, aes(x = temp9am, y = temp3pm)) +
  geom_point()

\(\text{likelihood model:} \; \; \; Y_i | \beta_0, \beta_1, \sigma \;\;\;\stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right)\text{ with } \mu_i = \beta_0 + \beta_1X_{i1}\)

\(\text{prior models:}\)

\(\beta_0\sim N(\ldots, \ldots )\)
\(\beta_1\sim N(\ldots, \ldots )\)
\(\sigma \sim \text{Exp}(\ldots)\)

weather_model_1 <- stan_glm(
  temp3pm ~ temp9am, 
  data = weather_WU, family = gaussian,
  prior_intercept = normal(25, 5),
  prior = normal(0, 2.5, autoscale = TRUE), 
  prior_aux = exponential(1, autoscale = TRUE),
  chains = 4, iter = 5000*2, seed = 84735, refresh = FALSE)

mcmc_dens_overlay(weather_model_1)

posterior_interval(weather_model_1, prob = 0.80)
                  10%      90%
(Intercept) 2.9498083 5.448752
temp9am     0.9802648 1.102423
sigma       3.8739305 4.409474

pp_check(weather_model_1)

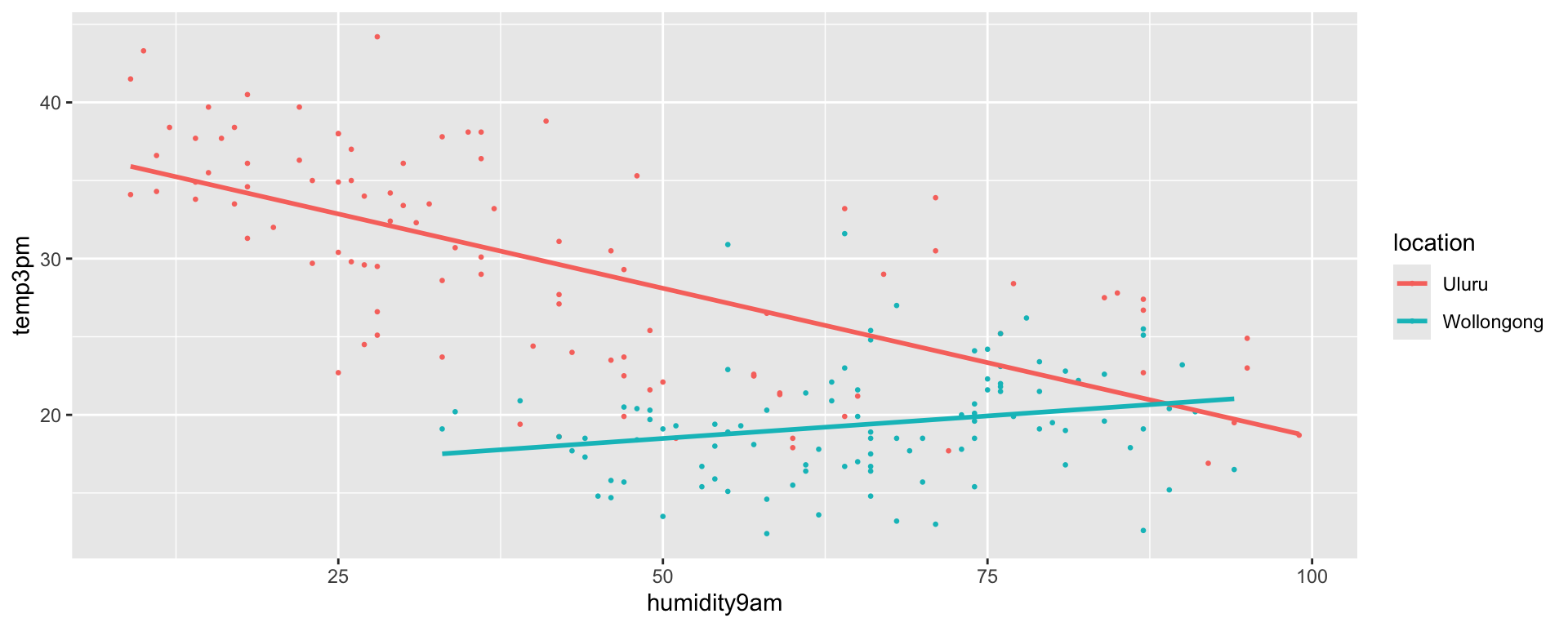
Considering a categorical predictor

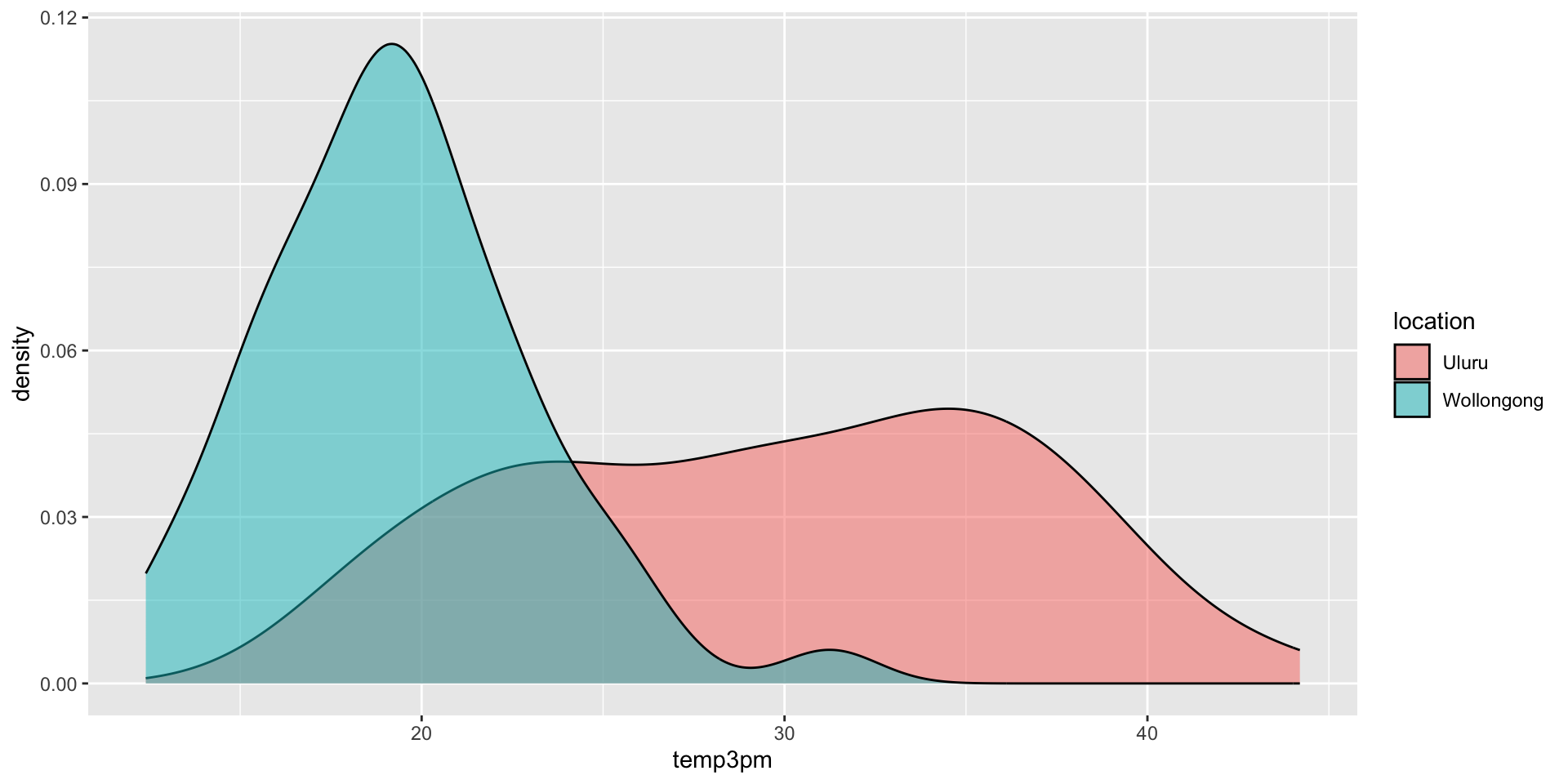
ggplot(weather_WU, aes(x = temp3pm, fill = location)) +
  geom_density(alpha = 0.5)

\[X_{i2} = \begin{cases} 1 & \text{ Wollongong} \\ 0 & \text{ otherwise (ie. Uluru)} \\ \end{cases}\]

\(\text{likelihood model:} \; \; \; Y_i | \beta_0, \beta_1, \sigma \;\;\;\stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right)\text{ with } \mu_i = \beta_0 + \beta_1X_{i2}\)

\(\text{prior models:}\)

\(\beta_0\sim N(\ldots, \ldots )\)
\(\beta_1\sim N(\ldots, \ldots )\)
\(\sigma \sim \text{Exp}(\ldots)\)

–

For Uluru, \(X_{i2} = 0\) and the trend in 3pm temperature simplifies to

\[\beta_0 + \beta_1 \cdot 0 = \beta_0 \; .\] For Wollongong, \(X_{i2} = 1\) and the trend in 3pm temperature is

\[\beta_0 + \beta_1 \cdot 1 = \beta_0 + \beta_1 \; .\]

Simulating the Posterior

weather_model_2 <- stan_glm(
  temp3pm ~ location,
  data = weather_WU, family = gaussian,
  prior_intercept = normal(25, 5),
  prior = normal(0, 2.5, autoscale = TRUE), 
  prior_aux = exponential(1, autoscale = TRUE),
  chains = 4, iter = 5000*2, seed = 84735, refresh = FALSE)

mcmc_dens_overlay(weather_model_2)

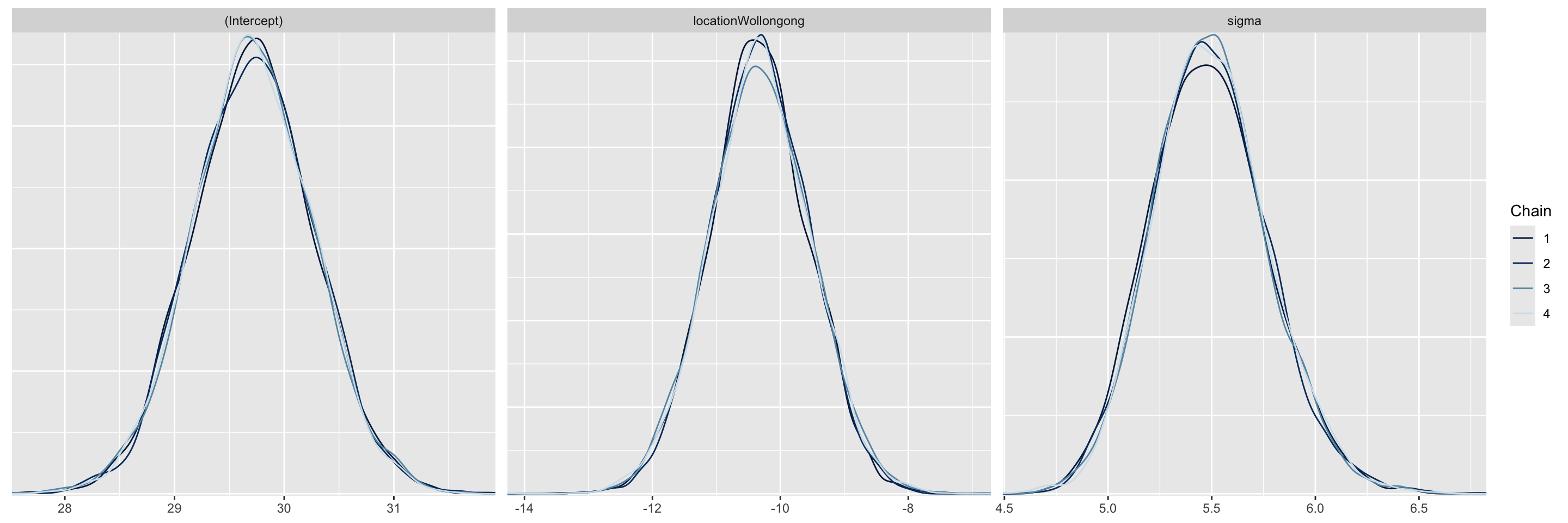
# Posterior summary statistics
model_summary <- summary(weather_model_2)
head(as.data.frame(model_summary), -2) %>% 
  select(mean, "10%", "90%", Rhat)
                         mean       10%       90%      Rhat
(Intercept)         29.718920  29.01943 30.424971 1.0000536
locationWollongong -10.317874 -11.31883 -9.301761 1.0001838
sigma                5.494874   5.14486  5.857824 0.9999858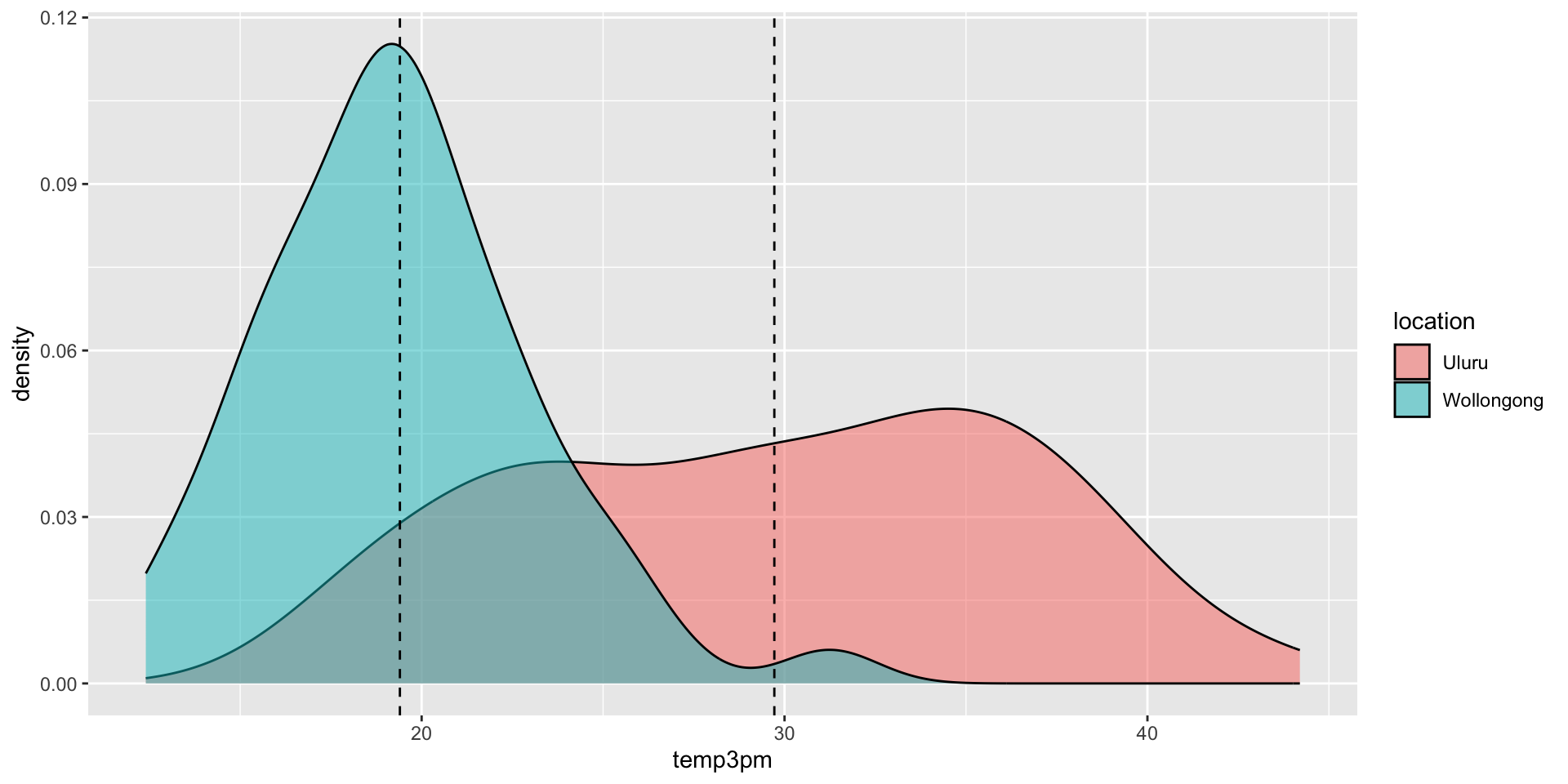
b0 <- model_summary[1,1]
b1 <- model_summary[2,1]

ggplot(weather_WU, aes(x = temp3pm, fill = location)) + 
  geom_density(alpha = 0.5) + 
  geom_vline(xintercept = c(b0, b0 + b1), 
    linetype = "dashed")

Two Predictors

ggplot(weather_WU, 
    aes(y = temp3pm, x = temp9am, color = location)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE)

\(\text{likelihood model:}\) \(Y_i | \beta_0, \beta_1, \beta_2 \sigma \;\;\;\stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right)\text{ with } \mu_i = \beta_0 + \beta_1X_{i1} + \beta_2X_{i2}\)

\(\text{prior models:}\)

\(\beta_0\sim N(m_0, s_0 )\)
\(\beta_1\sim N(m_1, s_1 )\)
\(\beta_2\sim N(m_2, s_2 )\)
\(\sigma \sim \text{Exp}(l)\)

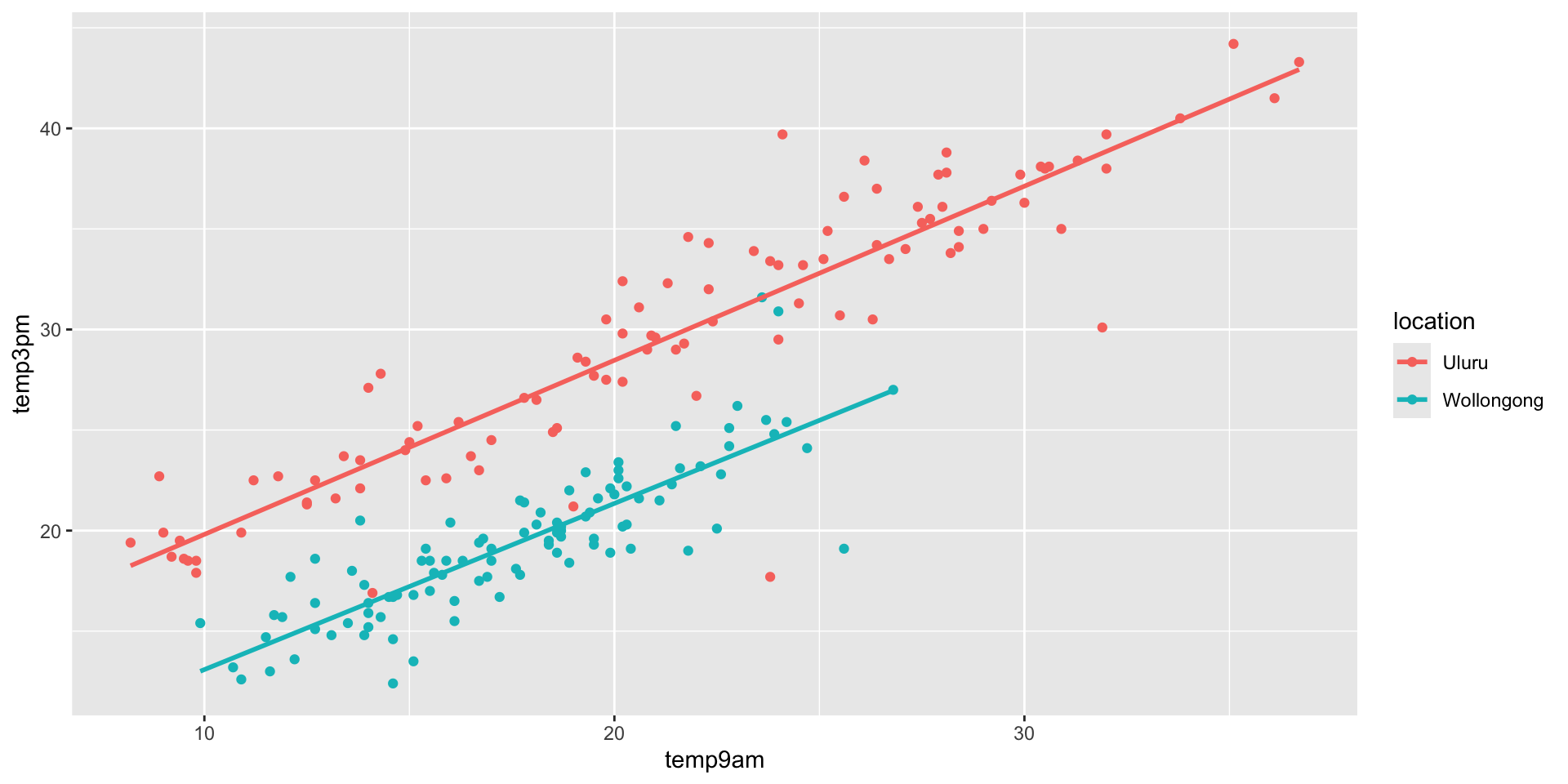
In Uluru, \(X_{i2} = 0\) and the trend in the relationship between 3pm and 9am temperature simplifies to

\[\beta_0 + \beta_1 X_{i1} + \beta_2 \cdot 0 = \beta_0 + \beta_1 X_{i1} \; .\]

In Wollongong, \(X_{i2} = 1\) and the trend in the relationship between 3pm and 9am temperature simplifies to

\[\beta_0 + \beta_1 X_{i1} + \beta_2 \cdot 1 = (\beta_0 + \beta_2) + \beta_1 X_{i1} \; .\]

weather_model_3 <- stan_glm(temp3pm ~ temp9am + location, 
                            data = weather_WU, 
                            family = gaussian, 
                            chains = 4, 
                            iter = 5000*2, 
                            seed = 84735,
                            refresh = FALSE)

weather_model_3_df <- as.data.frame(weather_model_3)
head(weather_model_3_df, 3)
  (Intercept)   temp9am locationWollongong    sigma
1    11.21958 0.8988170          -7.932687 2.588490
2    10.35556 0.9015759          -6.722425 2.559874
3    10.55716 0.8917270          -6.731531 2.556703

first_50 <- head(weather_model_3_df, 50)

ggplot(weather_WU, aes(x = temp9am, y = temp3pm)) + 
  geom_point(size = 0.01) + 
  geom_abline(data = first_50, size = 0.1,
    aes(intercept = `(Intercept)`, slope = temp9am)) + 
  geom_abline(data = first_50, size = 0.1,
    aes(intercept = `(Intercept)` + locationWollongong, 
    slope = temp9am), color = "blue")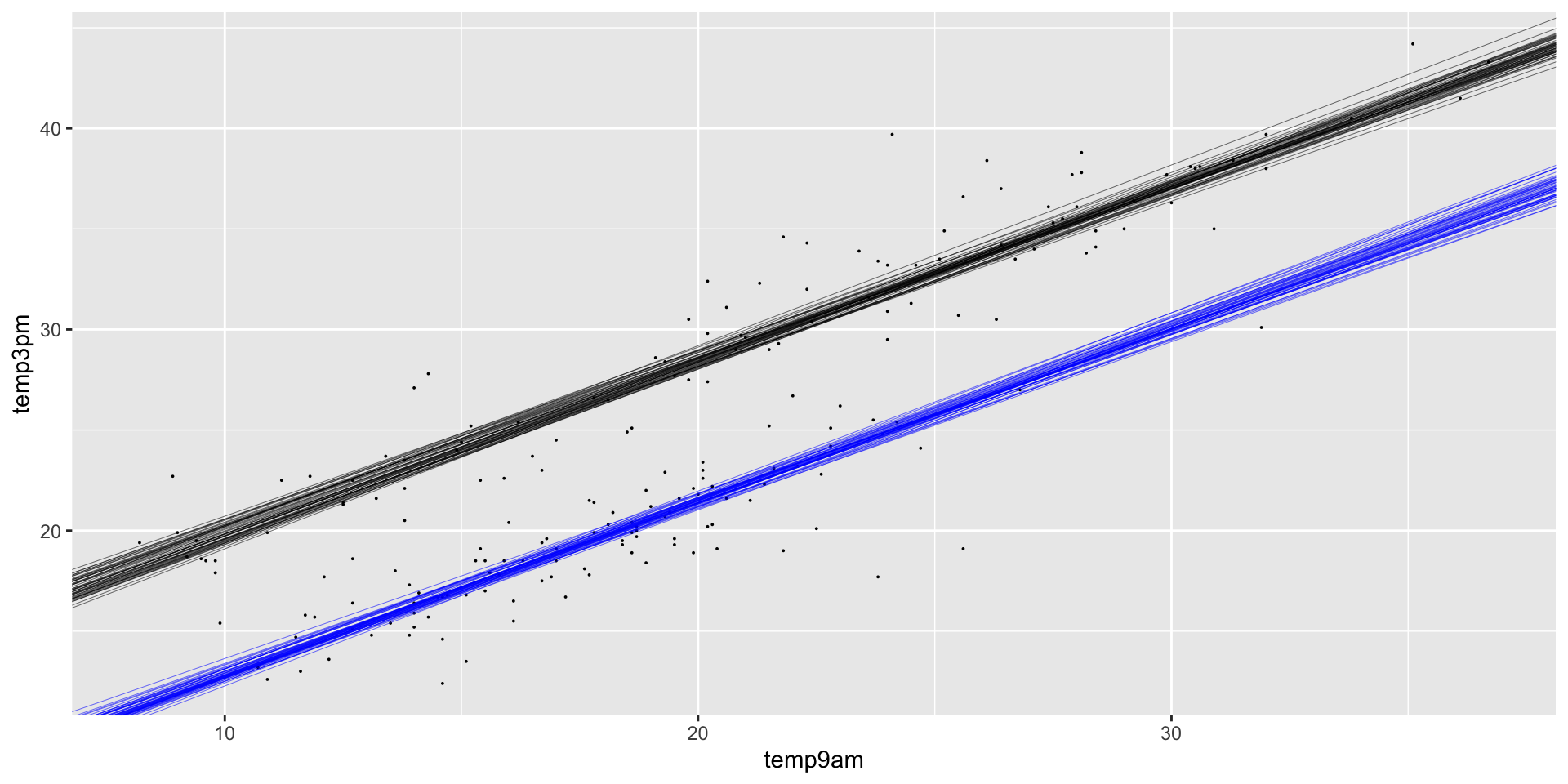

# Simulate a set of predictions
set.seed(84735)
temp3pm_prediction <- posterior_predict(
  weather_model_3, 
  newdata = data.frame(
    temp9am = c(10, 10), location = c("Uluru", "Wollongong")))

Posterior Predictive Model

shortcut_df <- data.frame(uluru = temp3pm_prediction[,1],
                          woll = temp3pm_prediction[,2])
ggplot(shortcut_df, aes(x = uluru)) +
  geom_density() +
  geom_density(aes(x = woll), color = "blue")

ggplot(weather_WU,
       aes(y = temp3pm, x = humidity9am, color = location)) + 
  geom_point(size = 0.5) +
  geom_smooth(method = "lm", se = FALSE)

\(\text{likelihood model:}\) \(Y_i | \beta_0, \beta_1, \beta_2, \beta_3 \sigma \;\;\;\stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right)\text{ with }\) \(\mu_i = \beta_0 + \beta_1X_{i2} + \beta_2X_{i3} + \beta_3X_{i2}X_{i3}\)

\(\text{prior models:}\)

\(\beta_0\sim N(m_0, s_0 )\)
\(\beta_1\sim N(m_1, s_1 )\)
\(\beta_2\sim N(m_2, s_2 )\)
\(\beta_3\sim N(m_3, s_3 )\)
\(\sigma \sim \text{Exp}(l)\)

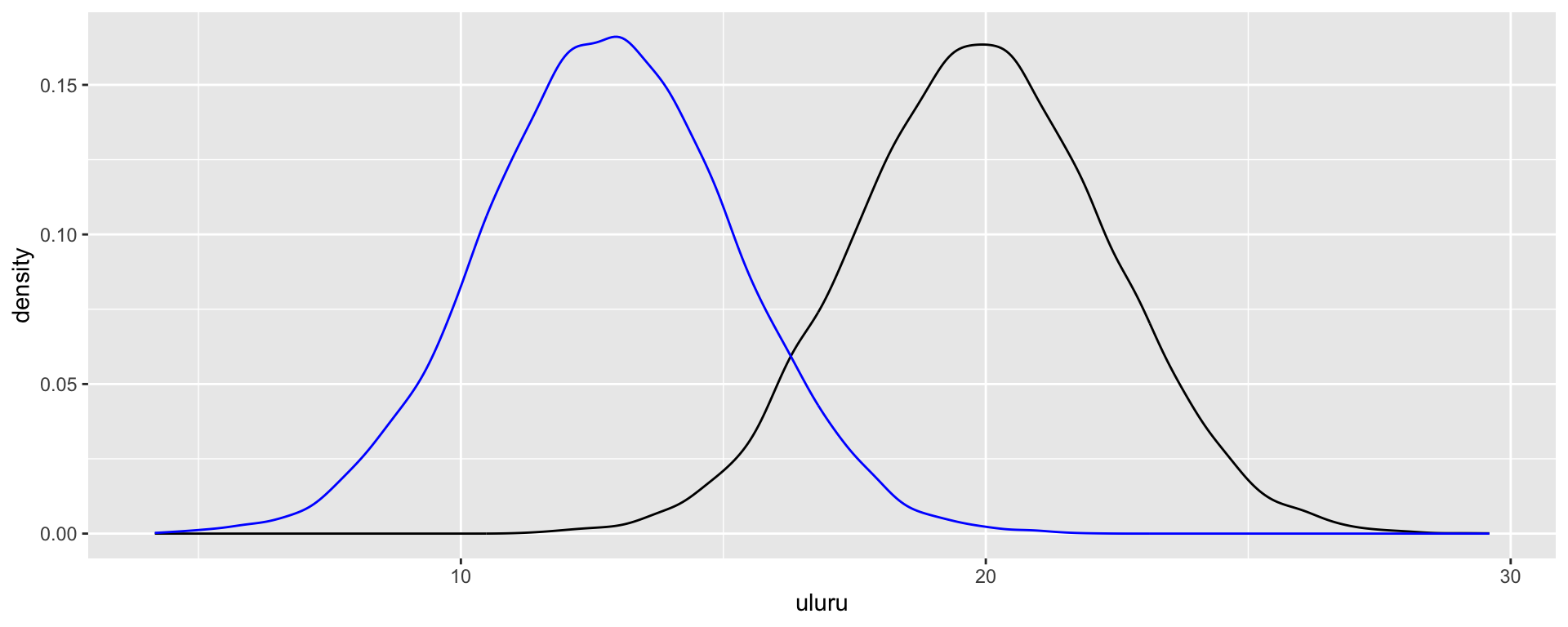
In Uluru, \(X_{2} = 0\) and the trend in the relationship between temperature and humidity simplifies to

\[\mu = \beta_0 + \beta_2 X_{3} \; .\]

In Wollongong, \(X_{2} = 1\) and the trend in the relationship between temperature and humidity simplifies to

\[\mu = \beta_0 + \beta_1 + \beta_2 X_{3} + \beta_3 X_{3} = (\beta_0 + \beta_1) + (\beta_2 + \beta_3) X_3 \; .\]

interaction_model <- stan_glm(temp3pm ~ location + humidity9am + 
                                location:humidity9am,
                              data = weather_WU, 
                              family = gaussian,
                              chains = 4, 
                              iter = 5000*2, 
                              seed = 84735)

model_summary <- summary(interaction_model)
head(as.data.frame(model_summary), -2) %>%
select(`10%`, `50%`, `90%`) %>%
round(3)
                                   10%     50%     90%
(Intercept)                     36.439  37.594  38.769
locationWollongong             -24.817 -21.890 -18.939
humidity9am                     -0.215  -0.190  -0.166
locationWollongong:humidity9am   0.199   0.246   0.293
sigma                            4.196   4.466   4.771

\[\begin{array}{lrl} \text{Uluru:} & \mu & = 37.594 - 0.19 \text{ humidity9am} \\ \text{Wollongong:} & \mu & = (37.594 - 21.89) + (-0.19 + 0.246) \text{ humidity9am}\\ && = 15.704 + 0.056 \text{ humidity9am}\\ \end{array}\]

Do you need an interaction term?

  • Context.

  • Visualizations.

  • Hypothesis tests.

More than two predictors

\(\text{likelihood model:} \; \; \; Y_i | \beta_0, \beta_1,\beta_2,...\beta_p, \sigma \;\;\;\stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right)\text{ with }\) \(\mu_i = \beta_0 + \beta_1X_{i1} + \beta_2X_{i2} + \ldots +\beta_pX_{ip}\)

\(\text{prior models:}\)

\(\beta_0, \beta_1,\beta_2, ...,\beta_p\sim N(\ldots, \ldots )\)

\(\sigma \sim \text{Exp}(\ldots)\)

weather_model_4 <- stan_glm(
  temp3pm ~ .,
  data = weather_WU, family = gaussian, 
  prior_intercept = normal(25, 5),
  prior = normal(0, 2.5, autoscale = TRUE), 
  prior_aux = exponential(1, autoscale = TRUE),
  chains = 4, iter = 5000*2, seed = 84735, refresh = FALSE)

Model evaluation and comparison

Model Formula
weather_model_1 temp3pm ~ temp9am
weather_model_2 temp3pm ~ location
weather_model_3 temp3pm ~ temp9am + location
weather_model_4 temp3pm ~ . 

set.seed(84735)
predictions_1 <- posterior_predict(weather_model_1, 
  newdata = weather_WU)
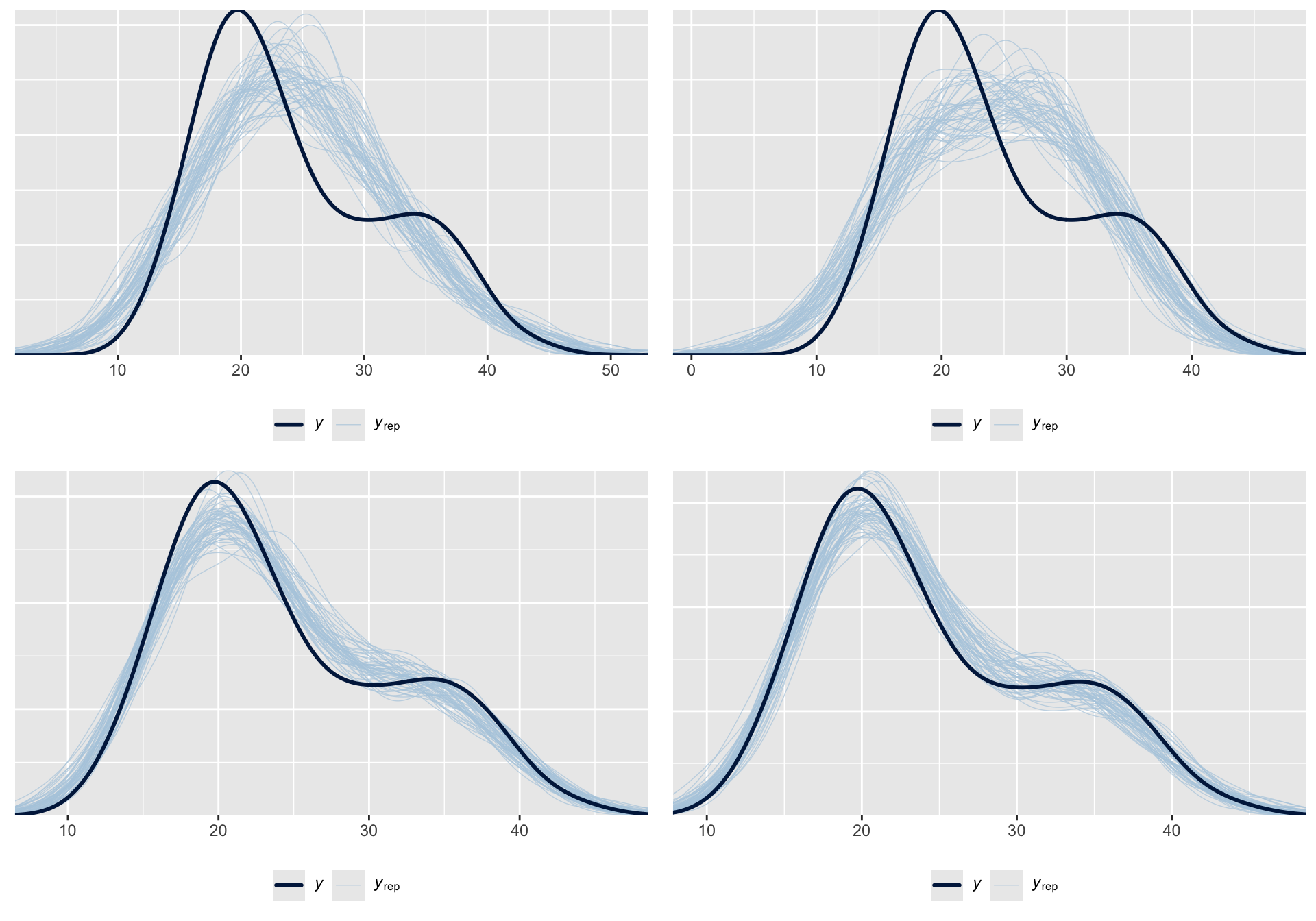
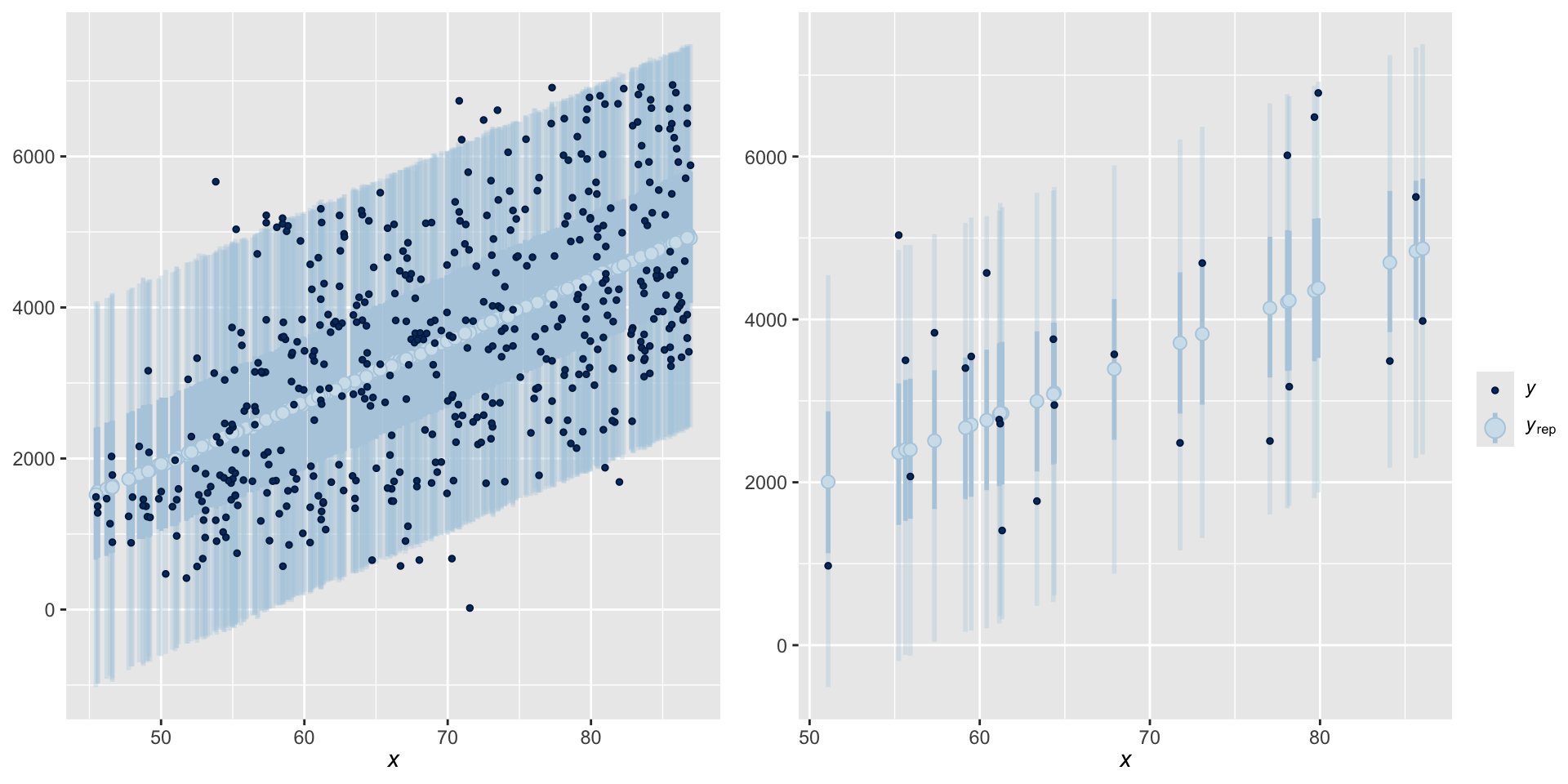
# Posterior predictive models for weather_model_1
ppc_intervals(weather_WU$temp3pm, 
  yrep = predictions_1, 
  x = weather_WU$temp9am, 
  prob = 0.5, prob_outer = 0.95)

# Posterior predictive models for weather_model_2
ppc_violin_grouped(weather_WU$temp3pm, 
  yrep = predictions_2, 
  group = weather_WU$location,
  y_draw = "points")

prediction_summary_cv(data = weather_WU, 
                      model = weather_model_1, 
                      k = 10)

model mae mae scaled within 50 within 95
weather model 1 3.285 0.79 0.405 0.97
weather model 2 3.653 0.661 0.495 0.935
weather model 3 1.142 0.483 0.67 0.96
weather model 4 1.206 0.522 0.64 0.95